記号・記法の約束 20200118 - (2nd) 檜山正幸のキマイラ飼育記

この記事のURL： https://m-hiyama-second.hatenablog.com/entry/2020/01/18/151235
ローカルファイル： YK-*/Notations2020.txt

$\newcommand{\hyph}{\mbox{-}} \newcommand{\vvec}[1]{{#1}\!\!\downarrow}$
内容：

行列の記法
点とベクトルの区別
内積と行列の掛け算
行列の成分表示
行列のサイズ
行列の等しさ
行列の和と積の成分表示
総和の性質

行列の記法

成分〈要素 | 項目 | 係数〉が集合Sの要素で、サイズがm行n列の行列の全体を Mat[S](n, m) と書く（n, mの順序に注意）。Mat[S](n, m) を $S[{}^m_n]$ とも書く。特に、

$S[{}^n_1] = Mat[S](1, n)$ 縦タプル
$S[{}^1_n] = Mat[S](n, 1)$ 横タプル

$S[{}^n_1]$ の要素を成分表示するときは、縦並び上付き添字にする。添字〈インデックス番号〉は上から下に向かって増える。

$x = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in S[^n_1]$

$S[{}^1_n]$ の要素を成分表示するときは、横並び下付き添字にする。添字〈インデックス番号〉は左から右に向かって増える。

$x = \begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix} \in S[_n^1]$

縦並びと横並びを区別するために、次のような注釈的飾り記号（矢印）を付けることがある。が、いつでも付けるとは限らない。（むしろ、たいていは付けない。）

縦並び $\vvec{x}$
横並び $\vec{x}$

つまり、

$x = \vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in S[^n_1] \\ \:\\ x = \vec{x} = \begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix} \in S[_n^1]$

$\vvec{x}$ は、世間ではほとんど使われてないので注意。縦でも横でも $\vec{x}$ で書くのが習慣。

多くの場合、成分の集合はR（実数）なので、 ${\bf R}[{}^m_n]$ を考える。

点とベクトルの区別

点の座標とベクトルの成分表示は、見た目で区別できない。区別したいときは、

点： $x = (x_1, x_2, \cdots, x_n)$
ベクトル： $\vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix}$

縦タプルを横書きで書きたいときは、

$x = \vvec{x} = [x^1, x^2, \cdots, x^n]^T$

Tは、transpose〈転置〉の't'から。

図形的な矢線ベクトルの成分表示は、原則として縦タプルを使う。

集合 Rⁿ が、点の座標の集合か、ベクトルの成分表示の集合かをどうしても区別したいときは、

点： ${\bf R}^n$
ベクトル： $\vvec{{\bf R}^n} = {\bf R}[^n_1]$

つまり、

点： $x = (x_1, x_2, \cdots, x_n) \in {\bf R}^n$
ベクトル： $x = \vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in \vvec{{\bf R}^n}$

内積と行列の掛け算

高校教科書で使われている「内積にドット」は使わない。ドットはスカラーや行列の掛け算記号に使う。

内積： (x|y)
掛け算（スカラー乗法〈倍〉、スカラー／行列の積）： x・y

掛け算記号の省略

スカラー・スカラーは多くの場合省略される。
スカラー・ベクトル、ベクトル・スカラーは多くの場合省略される。
行列・行列は多くの場合省略される。が、付けるときはドット。
内積と外積（外積は ^ または ×）は省略しない。

無闇に省略しすぎるとワケワカラナクなるので、演算子記号はある程度は付けたほうがよい。

行列の成分表示

縦方向に変化する添字〈インデックス〉は上付き、横方向に変化する添字〈インデックス〉は下付き。

$\begin{bmatrix} a^1_1 & a^1_2 & \ldots & a^1_n \\ \vdots & \vdots & \ddots & \vdots \\ a^m_1 & a^m_2 & \ldots & a^m_n \\ \end{bmatrix}$

次のような規則を設ける人もいるが、我々は守らない（どうせ守れないから）。文字の使用法は自由である。

行列は大文字、縦タプルは小文字、横タプルはギリシャ文字小文字（守らない！）
行列は大文字、その成分は小文字（無視！）

太字（ボールド体）、上に矢印などの書体・文字修飾も原則として使わない（気まぐれでたまに使うが）。

行列のサイズ

行列の行方向と列方向を憶えるには、「はじめての圏論その第2歩：行列の圏 - 檜山正幸のキマイラ飼育記 (はてなBlog)」に載せた次の絵：

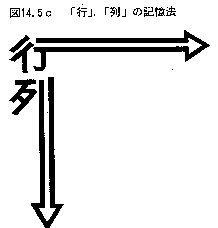
Aが行列のとき：

width(A) = Aの横幅 = Aの列数
height(A) = Aの縦高さ = Aの行数

「n×m 行列」という書き方は、列数〈幅〉・行数〈高さ〉がハッキリしないので、「n列m行行列」または「m行n列行列」を使う。

1行1列の行列とスカラーは区別する必要はない。（稀に区別することもあるが。）

行列の等しさ

スカラーの等しさは分かっているとして、行列の等しさ A = B は次のように定義する。

A と B のサイズは同じ（列数が同じかつ行数が同じ）
すべて i, j に対して $A_i^j = B_i^j$

AもBもn列m行だとすれば：

$A_i^j = B_i^j \:\:\:(1 \le i \le n,\: 1 \le j \le m)$

特に、縦タプルの等しさ x = y は：

$x^i = y^i \:\:\: (1 \le i \le n)$

横タプルの等しさ x = y は：

$x_i = y_i \:\:\: (1 \le i \le n)$

行列の和と積の成分表示

和：

$(A + B)_i^j = A_i^j + B_i^j$

特に、縦タプルと横タプルの和は：

$(x + y)^i = x^i + y^i$
$(x + y)_i = x_i + y_i$

積；

$(BA)_i^k = {\displaystyle \sum_{j = 1}^m} B_j^k A_i^j$

総和の性質

X, Y などは有限集合（リストだと思ってよい）で、f, g などは有限集合から実数への関数を表す。

$\displaystyle \sum_{x\in X}(f(x) + g(x)) = \sum_{x\in X}f(x) + \sum_{x\in X}g(x) \\$
$\displaystyle a\left(\sum_{x\in X}f(x)\right) = \sum_{x\in X}a f(x) \\$
$\displaystyle \left( \sum_{x\in X}f(x) \right)\left( \sum_{y\in Y} g(y)\right) = \sum_{x\in X} \sum_{y\in Y} f(x)g(y) = \sum_{(x, y)\in X\times Y} f(x)g(y)\\$
$\displaystyle \sum_{z \in X + Y}f(z) = \sum_{z \in X}f(z) + \sum_{z \in Y}f(z) \\$
$\displaystyle \sum_{(x, y) \in X \times Y}f(x, y) = \sum_{x \in X}\sum_{y \in Y}f(x, y) = \sum_{y \in Y}\sum_{x \in X}f(x, y) \\$

// 1 左辺
var sum = 0;
for (x in  X) {
  sum += (f(x) + g(x));
}
return sum;
// 1 右辺
var sum = 0;
for (x in  X) {
  sum += f(x);
}
for (x in  X) {
  sum += g(x);
}
return sum;

// 2 左辺
var sum = 0;
for (x in  X) {
  sum += f(x);
}
return a*sum;
// 2 右辺
var sum = 0;
for (x in  X) {
  sum += a*f(x);
}
return sum;

// 3 左辺
var sum_f = 0;
for (x in  X) {
  sum_f += f(x);
}
var sum_g = 0;
for (y in  Y) {
  sum_g += g(y);
}
return sum_f * sum_g;
// 3 右辺 1
var sum = 0;
for (x in  X) {
  for (y in Y) {
    sum += f(x)*g(y);
  }
}
return sum;
// 3 右辺 2
var sum = 0;
for (y in  Y) {
  for (x in X) {
    sum += f(x)*g(y);
  }
}
return sum;

// 4 左辺
var sum = 0;
for (z in  X + Y) {
  sum += f(z);
}
return sum;
// 4 右辺
var sum = 0;
for (z in  X) {
  sum += f(z);
}
for (z in  Y) {
  sum += f(z);
}
return sum;

// 5 左辺
var sum = 0;
for ([x, y] in X*Y) {
  sum += f([x, y]);
}
return sum;
// 5 右辺 1
var sum = 0;
for (x in X) {
  for (y in Y) {
    sum += f([x, y]);
  }
}
return sum;
// 5 右辺 2
var sum = 0;
for (y in Y) {
  for (x in X) {
    sum += f([x, y]);
  }
}
return sum;