復習と復讐〈リベンジ〉 1 (C A12P4) - (2nd) 檜山正幸のキマイラ飼育記

2020年1月19日に、簡単な自然変換の例を示そうと思ってトチったので、リベンジ。

圏論の抽象的概念も、具体例をたくさん触る（手でいじる）ことにより、だんだん実感がわいて、お馴染みのモノとなり、自由に扱えるようになる。考え込む前に例を作ろう。

内容：

習慣と設定
圏Cと圏D
関手 F
自然変換 α と、関手 G
自然性
練習問題と事例

習慣と設定

圏のあいだの関手〈functor〉は、英字〈ラテン文字〉大文字で書くのが習慣。
関手のあいだの自然変換〈natural transformation〉は、ギリシャ文字小文字で書くのが習慣。

習慣なので破っても問題ない。拘ったり絶対視してはいけない。

2つの関手 F, G:C→D のあいだの自然変換 α は、次のように書く。

α::F⇒G:C→D

縦に配置するなら：

 F:C→D
 ======= α
 G:C→D

F, G も縦書きすれば：

    C
  ---- F
    D
 ======= α
    C
  ---- G
    D

絵で描けば（ペースティング図とストリング図）：

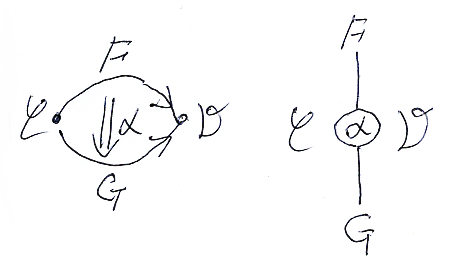
テキストでも絵でも、上下左右を入れ替えても読める／書けることが大事。例えば、ウィラートンは次のような絵を使う。

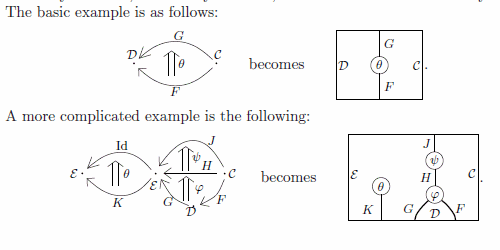
次の記事も参照。

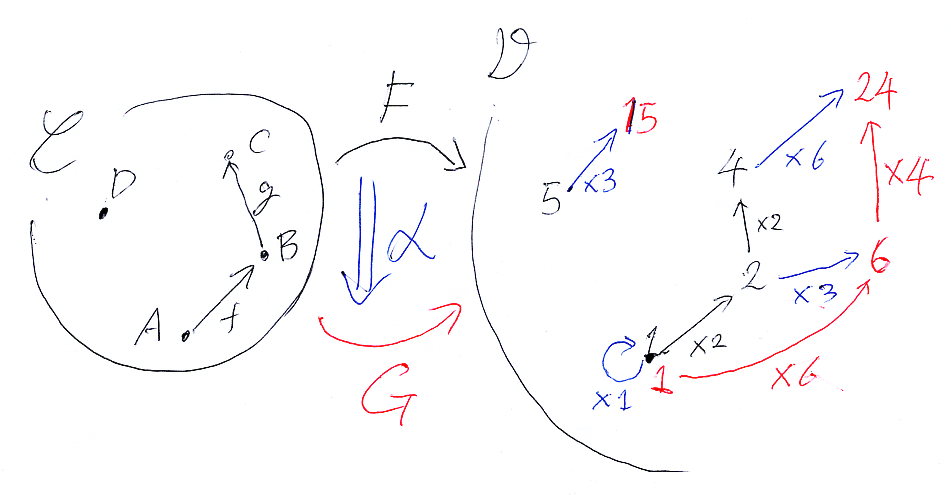
さて、C も D もやせた圏〈thin category〉の場合の事例を示す（次節以降）。やせた圏は単純なので、事例や実験をするには好適。以下の例は、C は適当なハッセ図から生成される圏、D は自然数の倍数約数順序から作られる圏とする。

圏Cと圏D

圏Cは、次の有向グラフ（ハッセ図）から生成される圏とする。図は、頂点が4個、辺が2本だが、圏に仕立てるには、恒等射と結合〈composition〉で作られる射を追加する。

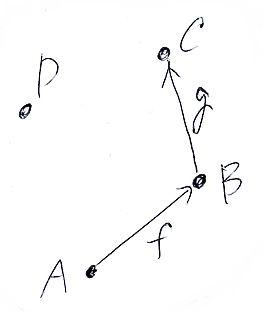
|C| = {A, B, C, D}
Mor(C) = {id_A, id_B, id_C, id_D, f, g, f;g}

f;g を h とも書くことにする。念の為に、7本の射の結合の演算表を書いてみる。x方向が→、y方向が↓として、x;y で欄を埋める。

	id_A	id_B	id_C	id_D	f	g	h
id_A	id_A
id_B		id_B			f
id_C			id_C			g	h
id_D				id_D
f	f
g		g			h
h	h

こういう作業をしてみるのも、具体例を触って慣れる行為の一環。手作業をしない限り慣れることは出来ない。

D は、自然数の倍数約数順序から作られるやせた圏。

|D| = N
Mor(D) = {(n, m)∈N×N | m は n の倍数 }
dom((n, m)) = n, cod((n, m)) = m
(ℓ, m);(m, n) = (ℓ, n)
id_n = (n, n)

これも、ハッセ図や演算表を書くなどの作業をして慣れる。

D の射は、n×k = m という掛け算の等式と1：1に対応する。例えば、

3×7 = 21 ←→ (3→21 in D)
5×2 = 10 ←→ (5→10 in D)

次のようにも書ける。

$\require{AMScd} \newcommand{\For}{\mbox{For}\:\:} \newcommand{\incat}{\:\: \mbox{in}\:} \newcommand{\cat}[1]{{\mathcal #1}} \begin{CD} 3 @>{\times 7}>> 21\incat \cat{D} \\ @. @. \\ 5 @>{\times 2}>> 10\incat \cat{D} \end{CD}$

D の射の名前の代わりに、掛け算の等式を使うことがある。

(3×7 = 21): 3→21 in D
(5×2 = 10): 5→10 in D

関手 F

関手 F を、次の図で定義する。

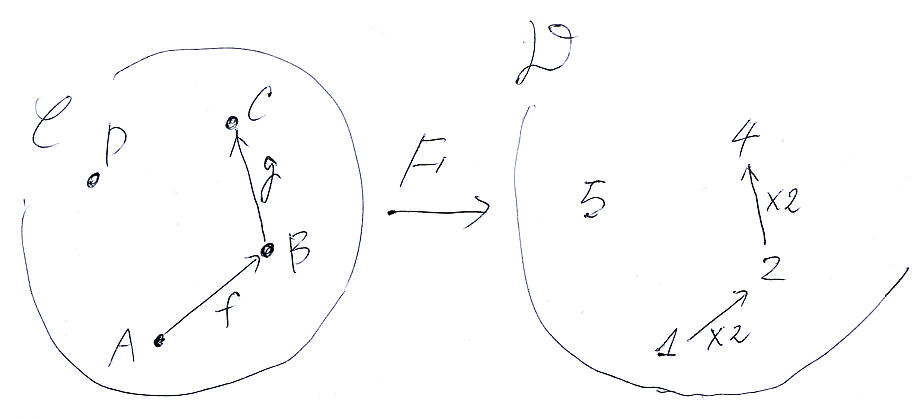
色々書き込むとゴチャゴチャするので、最小限の情報しか描いてない。次のとおり。

F(A) = 1
F(B) = 2
F(C) = 4
F(D) = 5
F(f:A→B) = (1×2 = 2)
F(g:B→C) = (2×2 = 4)

これだけ決めれば、恒等射と結合による射の値は自動的に決まる。例えば、

F(id_B) = id_F(B) = id₂ = (2×1 = 2)
F(h) = F(f;g) = F(f);F(g) = (1×2 = 2);(2×2 = 4) = (1×4 = 4)

自然変換 α と、関手 G

関手 G の定義をハッキリとは述べずに、自然変換 α を先に定義する。自然変換の実体は、C の対象に、D の射を割り当てる写像である。習慣により（破ってもいいが）、α(X) ではなくて α_X と書く。

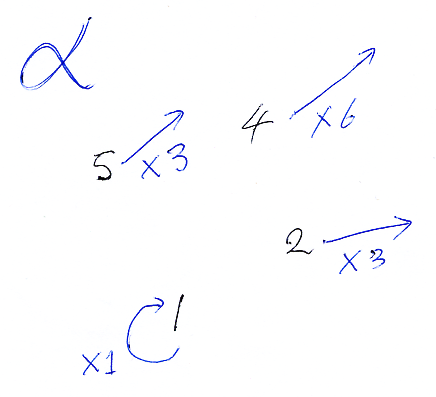
α_A = (1×1 = 1)
α_B = (2×3 = 6)
α_C = (4×6 = 24)
α_D = (5×3 = 15)

関手 G は、「F を α により移動〈変形〉した結果」のように考える。F を黒、α を青、G を赤で描くと：

自然性

やせた圏だけ相手にしていると自動的に満たされてしまうのだが、一般に、自然変換 α には次の可換図式が要求される。

$\For f:X \to Y \incat \cat{C} \\ \begin{CD} F(X) @>{\alpha_X}>> G(X) \\ @V{F(f)}VV @VV{G(f)}V \\ F(Y) @>{\alpha_Y}>> G(Y) \end{CD} \\ \mbox{commute} \incat \cat{D}$

この可換図式で表現される性質を自然性〈naturality〉と呼ぶ。当然ながら、この「自然性」はテクニカルターム〈専門用語〉であって、国語辞書的な「自然な感じ」とかではない！「なにゆえに“自然”と呼ぶのか」なんて問は無意味・不毛であって、上の可換図式が自然性の定義そのもの。

今回の例では自然性が成立するのは分かっているが、C の7本の射それぞれに対して可換図式を描いてみるのは良い練習。無理にでも機会を作って、可換図式／ストリング図を描いて、図式言語に慣れる。

C の射 id_A に対する自然性可換図式は：

$\begin{CD} F(A) @>{\alpha_A}>> G(A) \\ @V{F(id_A)}VV @VV{G(id_A)}V \\ F(A) @>{\alpha_A}>> G(A) \end{CD}$

値を代入すると：

$\begin{CD} 1 @>{\alpha_1}>> 1 \\ @V{id_1}VV @VV{id_1}V \\ 1 @>{\alpha_1}>> 1 \end{CD}$

α₁ も id₁ = (1×1 = 1) だから、

$\begin{CD} 1 @= 1 \\ @| @| \\ 1 @= 1 \end{CD}$

というツマラナイ可換図式になる。が、ツマラナイことになる事を理解することは大切。

C の射 f:A→B に対する自然性可換図式は：

$\begin{CD} F(A) @>{\alpha_A}>> G(A) \\ @V{F(f)}VV @VV{G(f)}V \\ F(B) @>{\alpha_B}>> G(B) \end{CD}$

値を代入すると：

$\begin{CD} 1 @>{\times 1}>> 1 \\ @V{\times 2}VV @VV{\times 6}V \\ 2 @>{\times 3}>> 6 \end{CD}$

C の射 g:B→C に対する自然性可換図式は：

$\begin{CD} F(B) @>{\alpha_B}>> G(B) \\ @V{F(g)}VV @VV{G(g)}V \\ F(C) @>{\alpha_C}>> G(C) \end{CD}$

値を代入すると：

$\begin{CD} 2 @>{\times 3}>> 6 \\ @V{\times 2}VV @VV{\times 4}V \\ 4 @>{\times 6}>> 24 \end{CD}$

他の射に対しても、同様に可換図式を描ける。

練習問題と事例

ここで具体的な問題を出すわけではないが、練習問題を自分で作ってやる。練習のやり方は、2020-1-19プリント（紙の印刷物）の「簡単な自然変換の事例（練習法）」に書いてある。今回のこの例を参考に、似た例を作って、自然性の可換図式も描いてみる。

自然変換の現実的な例は、次の記事内で「自然変換」を検索すれば見つかる。

また、2020-1-19プリントの次の宿題をやる。

「関手の例（宿題）」
「自然変換（導入）」の“宿題になるかも”