ブール値関数の基礎事項をまとめる。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in } }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%\newcommand{\When}{\Keyword{When } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
\newcommand{\Profile}{ \Keyword{Profile } }%
`$
一部の内容は以下と重複している。
上記記事では用語「述語」を使っている。この記事では「述語」を使わない。
内容:
いつものやり方
- プロファイリングする。
- 実例にあたる。実例をいじる。実例を手で触りながら進む。
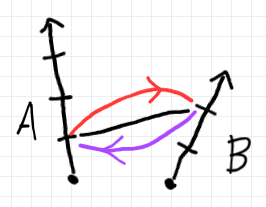
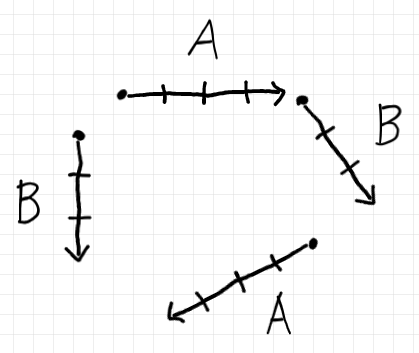
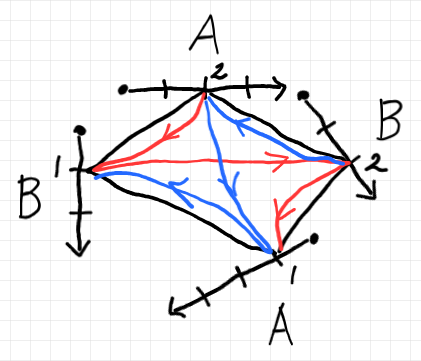
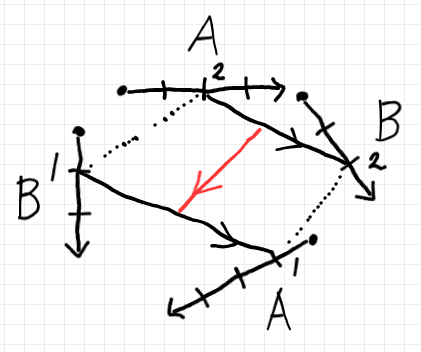
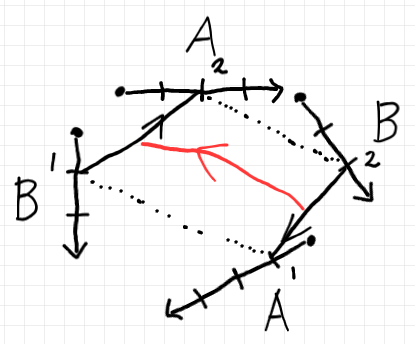
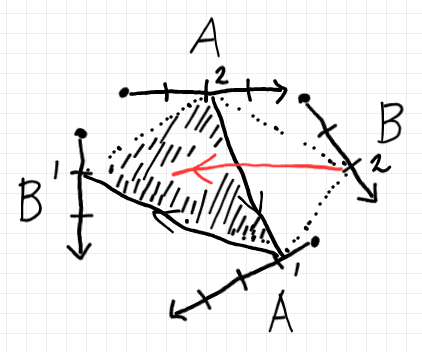
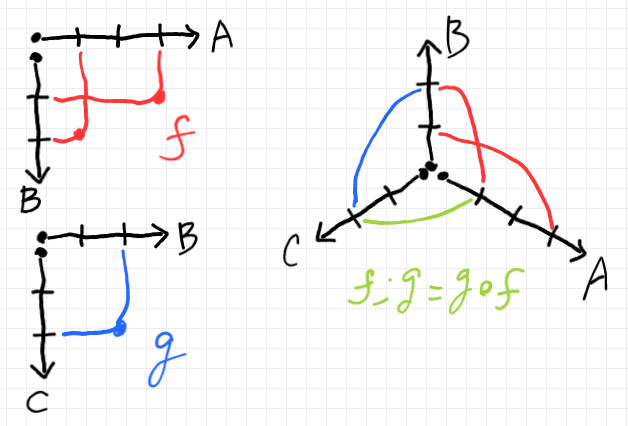
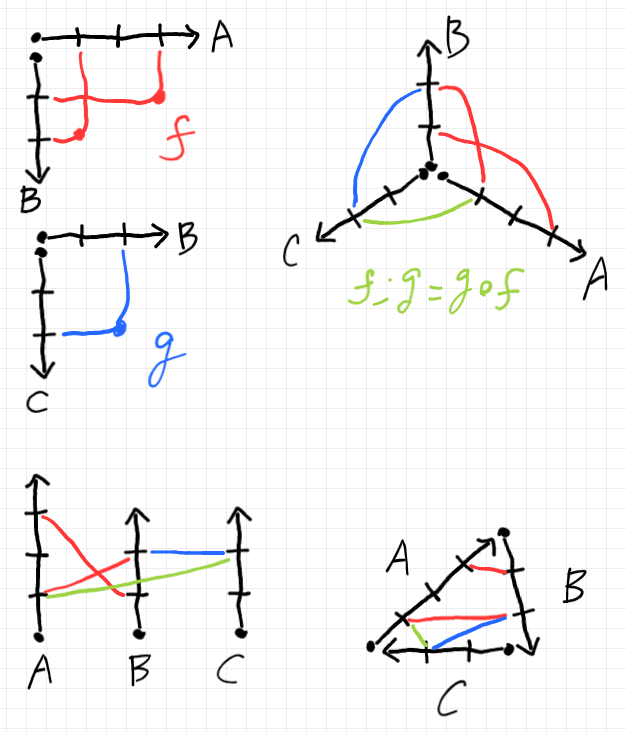
- 絵を描いてみる。→ 絵の描き方 2: 基本の描画法
- 文脈を読み取り、(忖度しながら)用語や記号を解釈する。
- 主観位置と視界を強く意識する。
- 空集合、単元集合を無視しない、バカにしない。
固有名の約束
空集合、単元集合、二元集合の固有名を次のように約束する。
- $`{\bf 0} := \{\}`$
- $`{\bf 1} := \{0\}`$ (唯一の要素は $`0`$)
- $`{\bf B} := \{0, 1\}`$
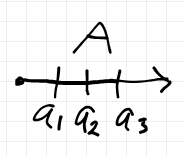
事例として三元集合もよく使うので、これも固有名を約束する。
- $`{\bf A} := \{1, 2, 3\}`$
フリップ付き半環としての二元集合
二元集合 $`{\bf B}`$ には 1 + 1 = 1 な足し算と普通の掛け算を入れて半環と考える。記号の乱用で次のように書く。
$`\quad {\bf B} = ({\bf B}, +, 0, \cdot, 1)`$
掛け算の演算記号 '$`\cdot`$' はしばしば省略される。$`{\bf B}`$ 上の関数 $`\mrm{flip}`$ を次のように定義する。
$`\Subject \mrm{flip}: {\bf B} \to {\bf B} \In {\bf Set}\\
\Define \mrm{flip} :=
\lambda\, x\in {\bf B}.(
\text{if } x= 0 \text{ then } 1 \text{ else } 0
)`$
なお、$`\text{if then else}`$ の代わりに次の書き方(関数値の列挙)も使う。
$`\quad\lambda\, x\in {\bf B}.(
0 \mapsto 1, 1 \mapsto 0
)`$
関数 $`\mrm{flip}`$ をフリップと呼ぶ。フリップも含めた半環を記号の乱用で次のように書く。
$`\quad {\bf B} = ({\bf B}, +, 0, \cdot, 1, \mrm{flip})`$
記号の乱用とは、ボールド体固有名 $`{\bf B}`$ が次の意味でオーバーロードされること。
1. 単なる二元集合
2. 足し算と掛け算を備えた半環
3. 足し算と掛け算とフリップを備えたフリップ付き半環〈semiring with flip〉
集合・関数の一般論から
バカみたいに簡単な集合・関数が、とんでもなく重要な役割りを演じる。重要な関数の名付け・書き方は習慣・伝統に従ったのでまったく統一性はない。一部ローカル記法もあり。
ポインティング関数〈pointing〉
次の同型がある。
$`\For X \in |{\bf Set}|\\
\quad X \cong \mrm{Map}({\bf 1}, X) \In {\bf Set}
`$
この同型を与える関数(左辺から右辺)をポインティング関数〈ポインティング写像〉と呼ぶ。
$`\For X \in |{\bf Set}|\\
\Subject \mrm{pointingMap}_X : X \to \mrm{Map}({\bf 1}, X) \In {\bf Set}\\
\For a\in X\\
\Define \mrm{pointingMap}_X(a) := (\, \lambda\, u\in {\bf 1}. a \,) \; \in \mrm{Map}({\bf 1}, X)
`$
$`X`$ も引数と考えた場合の $`\mrm{pointingMap}`$ のプロファイルは
$`\Profile \mrm{pointingMap} \in \prod_{X\in |{\bf Set}|} \mrm{Map}(\,X,\; \mrm{Map}({\bf 1}, X) \,)`$
$`\mrm{pointingMap}_X(a)`$ を $`a^\sim`$ と略記する。$`X`$ が何であっても次が成立する。
$`\quad \mrm{pointingMap}_X(a)(0) = a^\sim(0) = a \In X`$
評価関数〈evaluation〉
評価関数(俗称 エバル)は次のように定義する。
$`\For A, B \in |{\bf Set}|\\
\Subject \mrm{ev}_{A, B} : \mrm{Map}(A, B)\times A \to B \In {\bf Set}\\
\For f \in \mrm{Map}(A, B), a \in A\\
\Define \mrm{ev}_{A, B}(f, a) := f(a) \; \in B
`$
$`A, B`$ も引数と考えた場合の $`\mrm{ev}`$ のプロファイルは
$`\Profile \mrm{ev} \in \prod_{(A, B)\in |{\bf Set}|^2}\mrm{Map}(\, \mrm{Map}(A, B) \times A, \, B \,)`$
$`\mrm{ev}_{A, B}`$ の下付き $`A, B`$ はしばしば省略される。
等値関数〈equality〉
等値関数(イコール)は次のように定義する。
$`\For X \in |{\bf Set}|\\
\Subject \mrm{eq}_{X} : X\times X \to {\bf B} \In {\bf Set}\\
\For x, y \in X\\
\Define \mrm{eq}_{X}(x, y) := (x = y) \; \in {\bf B}
`$
イコール記号「$`=`$」は、素朴集合論により定義されているとして、それ以上詮索しない。
$`X`$ も引数と考えた場合の $`\mrm{eq}`$ のプロファイルは
$`\Profile \mrm{eq} \in \prod_{X \in |{\bf Set}|}\mrm{Map}(\, X \times X, \, {\bf B} \,)`$
$`\mrm{eq}_X`$ の下付き $`X`$ はしばしば省略される。イコール記号「$`=`$」と関数記号「$`\mrm{eq}`$」は完全に同義である。次は完全に同じで、書き方の流儀が違うだけで区別しない。
- $`x = y`$
- $`(=)(x , y)`$
- $`\mrm{eq}(x, y)`$
指示関数〈indicator〉
Wikipedia項目「指示関数」 より画像コピー:
注目点はギリシャ文字カイが使われていること。カイを使うのはかなり古くからの習慣。だが、全体集合が暗黙化されるのがちと困る。ここでは、全体集合を(必要なら)上付きで書く: $`\chi_A = \chi^X_A`$ 。
$`X`$ も引数と考えた場合の指示関数 $`\chi`$ のプロファイルは
$`\Profile \chi \in \prod_{X \in |{\bf Set}|}\mrm{Map}(\, \mrm{Pow}(X), \, \mrm{Map}(X, {\bf B}) \,)`$
指示関数でも、省略の程度や書き方の流儀の違いはあるだろう。次は区別しない。引数渡し構文は完全に恣意的(根拠なく偶然で決まる)。
- $`\chi_A, \, \chi_A(x)`$
- $`\chi_A^X, \, \chi_A^X(x)`$
- $`\chi^X(A), \, \chi^X(A)(x)`$
バン関数〈bang〉
ビックリマーク「!」を読み上げるとき「バン〈bang〉」とも読む。「#!」なら「ハッシュ・バン」、特殊な用途があるのでシバン〈シェバン〉と発音する。
$`!_X`$ は「バン・ローワーエックス」「バン・エックス」と読む。
バン関数は次のように定義する。
$`\For X \in |{\bf Set}|\\
\Subject \mrm{bang}_{X} : X \to {\bf 1} \In {\bf Set}\\
\Define \mrm{bang}_{X} := (\lambda\ x\in X.0) \; \in \mrm{Map}(X, {\bf 1})
`$
バン関数は終射〈terminal {morphism | map}〉とも呼ぶ(別名、同義語)。もちろん $`!_X`$ と略記する
$`X`$ も引数と考えた場合のバン関数のプロファイルは
$`\Profile \mrm{bang} \in \prod_{X \in |{\bf Set}|}\mrm{Map}(\, X, \, {\bf 1} \,)`$
定数値関数〈constant〉
ドイツ語では konstant 、Kを使うのは伝統。定数値関数は次のように定義する。
$`\For A, B \in |{\bf Set}|\\
\For b \in B\\
\Subject \mrm{K}_{A, B}^b : A \to B \In {\bf Set}\\
\Define \mrm{K}_{A, B}^b := (\lambda\, x\in A. b) \; \in \mrm{Map}(A, B)
`$
$`A, B`$ も引数と考えた場合の定数値関数 $`\mrm{K}`$ のプロファイルは
$`\Profile \mrm{K} \in \prod_{(A, B) \in |{\bf Set}|^2} \mrm{Map}(\,B, \, \mrm{Map}(A, B) \,)`$
逆像関数と像関数
$`f:A \to B \In {\bf Set}`$ に対して $`f^{-1}`$ は幾つかの意味でオーバーロードされる。そのなかの3つの用法(他の用法もある)。
- 逆関数: $`f^{-1} : B \to A \In {\bf Set}`$
- 要素の逆像関数: $`f^{-1} : B \to \mrm{Pow}(A) \In {\bf Set}`$
- 部分集合の逆像関数: $`f^{-1} : \mrm{Pow}(B) \to \mrm{Pow}(A) \In {\bf Set}`$
ここでは、$`f^{-1}`$ を要素の逆像関数として使う。
部分集合の像関数〈順像関数〉も使うが、同じ名前 $`f`$ をオーバーロードする。
- 像関数〈順像関数〉: $`f: \mrm{Pow}(A) \to \mrm{Pow}(B) \In {\bf Set}`$
単元集合上のブール値関数
次が成立する。
- $`\mrm{Map}({\bf 1}, {\bf B}) \cong \mrm{Pow}( {\bf 1}) \In {\bf Set}`$ (関数-部分集合)
- $`(0\mapsto 0) \longleftrightarrow \{\} = {\bf 0}`$
- $`(0\mapsto 1) \longleftrightarrow \{0\} = {\bf 1}`$
- $`\mrm{Map}({\bf 1}, {\bf B}) \cong {\bf B} \In {\bf Set}`$ (関数-値)
- $`(0\mapsto 0) \longleftrightarrow 0`$
- $`(0\mapsto 1) \longleftrightarrow 1`$
一番目の関数-部分集合・同型(関数から部分集合)を与える関数は
$`\Subject \mrm{InvImg1} : \mrm{Map}({\bf 1}, {\bf B}) \to \mrm{Pow}({\bf 1}) \In {\bf Set}\\
\For f \in \mrm{Map}({\bf 1}, {\bf B})\\
\Define \mrm{InvImg1}(f) := f^{-1}(1) \; \in \mrm{Pow}({\bf 1})
`$
$`\mrm{InvImg1}`$ は inverse image of 1 から。$`(\hyp^{-1})(1)`$ と完全に同義だが、あえて名前を付けた。
一番目の関数-部分集合・同型(部分集合から関数)を与える関数は、
$`\Subject \mrm{SubsetToPointing} : \mrm{Pow}({\bf 1}) \to \mrm{Map}({\bf 1}, {\bf B}) \In {\bf Set}\\
\For A \in \mrm{Pow}({\bf 1})\\
\Define \mrm{SubsetToPointing}(A) := \chi^{\bf 1}_A \; \in \mrm{Map}({\bf 1}, {\bf B})
`$
$`\mrm{SubsetToPointing}`$ は $`\chi^{\bf 1}_\hyp`$ と完全に同義だが、あえて名前を付けた。指示関数〈indicator function〉とブール値ポインティング関数が同じになる($`\mrm{Map}({\bf 1}, {\bf B})`$ の要素)のは単元集合特有。
ニ番目の関数-値・同型(関数から値)を与える関数は
$`\Subject \mrm{ev0} : \mrm{Map}({\bf 1}, {\bf B}) \to {\bf B} \In {\bf Set}\\
\For f \in \mrm{Map}({\bf 1}, {\bf B})\\
\Define \mrm{ev0}(f) := \mrm{ev}(f, 0) \; \in {\bf B}
`$
$`\mrm{ev0}`$ は evaluation at 0 から。$`\mrm{ev}(\hyp, 0)`$ と完全に同義だが、あえて名前を付けた。
ニ番目の関数-値・同型(値から関数)を与える関数は
$`\Subject \mrm{ValToPointing} : {\bf B} \to \mrm{Map}({\bf 1}, {\bf B}) \In {\bf Set}\\
\For x \in {\bf B}\\
\Define \mrm{valToPointing}(x) := \mrm{pointingMap}_{\bf B}(x) \; \in \mrm{Map}({\bf 1}, {\bf B})
`$
$`\mrm{ValToPointing}`$ は $`\mrm{pointingMap}_{\bf B}(\hyp)`$ と完全に同義だが、あえて名前を付けた。
図式としてまとめると:
$`\quad \xymatrix@R+4pc@C+2pc{
{}
&{\mrm{Map}({\bf 1}, {\bf B})} \ar@/_1.5pc/[dl]_-{\mrm{InvImg1}}
\ar@/^1.5pc/[dr]^-{\mrm{ev0}}
&{}
\\
{\mrm{Pow}({\bf 1})} \ar@/_1.5pc/[ur]|{\mrm{SubsetToPointing}}
& {}
& {\bf B} \ar@/^1.5pc/[ul]|{\mrm{ValToPointing}} \ar@{.>}[ll]^{\mrm{bold}}
}\\
\quad \text{commutative } \In {\bf Set}
`$
点線の関数 $`\mrm{bold}`$ は定義してないが、次の関数。
$`\Subject \mrm{bold} : {\bf B} \to \mrm{Pow}({\bf 1}) \In {\bf Set}\\
\Define \mrm{bold} := \lambda\, x\in {\bf B}.(0 \mapsto {\bf 0}, 1\mapsto {\bf 1})
`$
見た目上、普通のフォントをボールドフォント〈太字〉に変えているだけなので、関数名を 'bold' にした。$`\mrm{bold}`$ の逆関数(逆像関数ではない!)$`\mrm{unbold}`$ も容易に定義できる。
$`\Profile \mrm{unbold} : \mrm{Pow}({\bf 1}) \to {\bf B} \In {\bf Set}`$
関数のペアが互いに逆で、同型を与えることは次のように書ける。
- $`\mrm{InvImg1};\mrm{SubsetToPointing} = \id_{\mrm{Map}({\bf 1}, {\bf B})} \In {\bf Set}`$
- $`\mrm{SubsetToPointing}; \mrm{InvImg1}; = \id_{\mrm{Pow}({\bf 1})} \In {\bf Set}`$
- $`\mrm{ev0} ; \mrm{ValToPointing} = \id_{ \mrm{Map}({\bf 1}, {\bf B})} \In {\bf Set}`$
- $`\mrm{ValToPointing}; \mrm{ev0} = \id_{{\bf 1} } \In {\bf Set}`$
- $`\mrm{bold}; \mrm{unbold} = \id_{\bf B}`$
- $`\mrm{unbold}; \mrm{bold} = \id_{\mrm{Pow}({\bf B})}`$
一般の集合上のブール値関数
単元集合とは限らない集合 $`X`$ では次は成立しない(正確に言えば「常に成立することを保証できない」)。
- $`\mrm{Mpa}(X, {\bf B}) \cong \mrm{Pow}({\bf 1}) \In {\bf Set}`$
- $`\mrm{Mpa}(X, {\bf B}) \cong {\bf B} \In {\bf Set}`$
上の2つが成立しないことを、まとめて次のような日本語で表現する。
- 一般に、$`X`$ 上のブール値関数は2つだけとは限らない。2つ以上のブール値関数があるかも知れない。
例 1: $`{\bf A} = \{1, 2, 3\}`$ 上のブール値関数は $`2^3 = 8`$ 個ある。
例 2: 空集合 $`\{\}`$ 上のブール値関数は1個だけある。
例 3: 二元集合 $`{\bf B}`$ 上のブール値関数は4個ある。
例 4: 四元集合 $`{\bf B}\times {\bf B}`$ 上のブール値関数は16個ある。幾つかを行列として書いてみると: $`\begin{bmatrix} 0 & 0 \\ 0 & 0\end{bmatrix},
\begin{bmatrix} 0 & 1 \\ 0 & 0\end{bmatrix},
\begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix},
\begin{bmatrix} 1 & 1 \\ 1 & 1\end{bmatrix}
`$
例 5: $`\mrm{Map}({\bf A}, {\bf B})`$ 上のブール値関数は $`2^8 = 2^4 \times 2^4 = 256`$ 個ある。8ビット = 1バイト のデジタルデータとしてエンコードできる。関数ごとに256色の一色を担当色に割り当てることができる。→ 8ビットカラー、メンバーカラー、担当カラー
注意: 例 5 の $`\mrm{Map}(\mrm{Map}({\bf A}, {\bf B}), {\bf B})`$ の要素(256個ある)は、ブール値関数を引数にもらってブール値を返すので、メタ・ブール値関数とも呼ぶ。「メタ」は「高階」と同義で、それ以上でもそれ以下でもない(単なる形容詞)。$`\mrm{Map}(\mrm{Map}({\bf 1}, {\bf B}), {\bf B})`$ の要素も定義上メタ・ブール値関数である($`{\bf 1}`$ をのけ者扱いしない!)。$`\mrm{Map}(\mrm{Map}({\bf 0}, {\bf B}), {\bf B})`$ の要素も定義上メタ・ブール値関数である($`{\bf 0}`$ をのけ者扱いしない!)。
単元集合では事情が特殊だった。
- 単元集合上では、ブール値関数はちょうど2つだけである。その2つはブール値と同一視できる。
一般の集合 $`X`$ でも次は成立する。
- $`\mrm{Mpa}(X, {\bf B}) \cong \mrm{Pow}({X})`$ (一般の関数-部分集合)
次のように図示できる。
$`\quad \xymatrix@R+4pc@C+2pc{
{}
&{\mrm{Map}(X, {\bf B})} \ar@/_1.5pc/[dl]_-{\mrm{InvImg1}_X}
\ar[dr]^{\mrm{ev}_{X, {\bf B}}(\hyp, a)}
&{}
\\
{\mrm{Pow}(X)} \ar@/_1.5pc/[ur]|{\mrm{SubsetToIndicator}_X}
& {}
& {\bf B}
}\\
\quad \text{commutative } \In {\bf Set}
`$
関数 $`\mrm{InvImg1}_X, \mrm{SubsetToIndicator}_X, \mrm{ev}_{X, {\bf B}}(\hyp, a)`$ の定義は単元集合の場合と変わらない。定義は省略する。具体例を挙げる。
集合 $`{\bf A}`$ 上のブール値関数は、次の形で書ける。
$`\quad \lambda\, x\in {\bf A}.(
1 \mapsto 0, 2 \mapsto 1, 3 \mapsto 1
)`$
これを次の形に略記する(ここだけ一時的)。
$`\quad \mrm{fun}(0, 1, 1) : {\bf A} \to {\bf B} \In {\bf Set}`$
$`\mrm{InvImg1}_{\bf A}`$ の値を全部列挙する。
- $`\mrm{InvImg1}(\mrm{fun}(0, 0, 0)) = \{\}`$
- $`\mrm{InvImg1}(\mrm{fun}(1, 0, 0)) = \{1\}`$
- $`\mrm{InvImg1}(\mrm{fun}(0, 1, 0)) = \{2\}`$
- $`\mrm{InvImg1}(\mrm{fun}(0, 0, 1)) = \{3\}`$
- $`\mrm{InvImg1}(\mrm{fun}(1, 1, 0)) = \{1, 2\}`$
- $`\mrm{InvImg1}(\mrm{fun}(1, 0, 1)) = \{1, 3\}`$
- $`\mrm{InvImg1}(\mrm{fun}(0, 1, 1)) = \{2, 3\}`$
- $`\mrm{InvImg1}(\mrm{fun}(1, 1, 1)) = \{1, 2, 3\}`$
$`\mrm{SubsetToIncicatro}_{\bf A}`$ の値を全部列挙する。
- $`\mrm{SubsetToIncicatro}(\{\}) = \mrm{fun}(0, 0, 0)`$
- $`\mrm{SubsetToIncicatro}(\{1\}) = \mrm{fun}(1, 0, 0)`$
- $`\mrm{SubsetToIncicatro}(\{2\}) = \mrm{fun}(0, 1, 0)`$
- $`\mrm{SubsetToIncicatro}(\{3\}) = \mrm{fun}(0, 0, 1)`$
- $`\mrm{SubsetToIncicatro}(\{1, 2\}) = \mrm{fun}(1, 1, 0)`$
- $`\mrm{SubsetToIncicatro}(\{1, 3\}) = \mrm{fun}(1, 0, 1)`$
- $`\mrm{SubsetToIncicatro}(\{2, 3\}) = \mrm{fun}(0, 1, 1)`$
- $`\mrm{SubsetToIncicatro}(\{1, 2, 3\}) = \mrm{fun}(1, 1, 1)`$
要するに:
- $`\mrm{fun}(0, 0, 0) \longleftrightarrow \{\}`$
- $`\mrm{fun}(1, 0, 0) \longleftrightarrow \{1\}`$
- $`\mrm{fun}(0, 1, 0) \longleftrightarrow \{2\}`$
- $`\mrm{fun}(0, 0, 1) \longleftrightarrow \{3\}`$
- $`\mrm{fun}(1, 1, 0) \longleftrightarrow \{1, 2\}`$
- $`\mrm{fun}(1, 0, 1) \longleftrightarrow \{1, 3\}`$
- $`\mrm{fun}(0, 1, 1) \longleftrightarrow \{2, 3\}`$
- $`\mrm{fun}(1, 1, 1) \longleftrightarrow \{1, 2, 3\}`$
これで、次の同型を具体的に確認した。
$`\quad \mrm{Map}({\bf A}, {\bf B}) \cong \mrm{Pow}({\bf A}) \In {\bf Set}`$
ゼロ、ワン、ワンの選択
$`\For X\in |{\bf Set}|\\
\Subject \mrm{Zero}_X : X \to {\bf B} \In {\bf Set}\\
\Define \mrm{Zero}_X := (\lambda\, x\in X.0) \; \in \mrm{Map}(X, {\bf B})
`$
$`\For X\in |{\bf Set}|\\
\Subject \mrm{One}_X : X \to {\bf B} \In {\bf Set}\\
\Define \mrm{One}_X := (\lambda\, x\in X.1) \; \in \mrm{Map}(X, {\bf B})
`$
$`\mrm{Zero}_X, \mrm{One}_X`$ の下付き $`X`$ は省略することがある。$`\mrm{Zero}_X, \mrm{One}_X`$ は定数値関数/指示関数だから、次が成立する。
$`\quad \mrm{Zero}_X = \mrm{K}_{X, {\bf B}}^0 \; : X \to {\bf B} \In {\bf Set}\\
\quad \mrm{One}_X = \mrm{K}_{X, {\bf B}}^1 \; : X \to {\bf B} \In {\bf Set}\\
\quad \mrm{Zero}_X = \chi^X_{\bf 0} \; : X \to {\bf B} \In {\bf Set} \\
\quad \mrm{One}_X = \chi^X_X \; : X \to {\bf B} \In {\bf Set}
`$
$`X = {\bf 1}`$ と置いても、もちろんよい。
$`\Profile \mrm{Zero}_{\bf 1} : {\bf 1} \to {\bf B} \In {\bf Set} \\
\Profile \mrm{One}_{\bf 1} : {\bf 1} \to {\bf B} \In {\bf Set}
`$
次が成立する。
$`\quad \mrm{Zero}_{\bf 1} = 0^\sim \; : {\bf 1} \to {\bf B} \In {\bf Set} \\
\quad \mrm{One}_{\bf 1} = 1^\sim \; : {\bf 1} \to {\bf B} \In {\bf Set} \\
\quad \mrm{Zero}_{\bf 1} = \mrm{K}_{{\bf 1}, {\bf B}}^0 \; : {\bf 1} \to {\bf B} \In {\bf Set}\\
\quad \mrm{One}_{\bf 1} = \mrm{K}_{{\bf 1}, {\bf B}}^1 \; : {\bf 1} \to {\bf B} \In {\bf Set}\\
\quad \mrm{Zero}_{\bf 1} = \chi^{\bf 1}_{\bf 0} \; : {\bf 1} \to {\bf B} \In {\bf Set} \\
\quad \mrm{One}_{\bf 1} = \chi^{\bf 1}_{\bf 1} \; : {\bf 1} \to {\bf B} \In {\bf Set}
`$
$`\mrm{Map}(X, {\bf B})`$ 上のブール値関数 $`\mrm{PickOne}_X`$ を定義する。
$`\For X\in |{\bf Set}|\\
\Subject \mrm{PickOne}_X : \mrm{Map}(X, {\bf B}) \to {\bf B} \In {\bf Set}\\
\Define \mrm{PickOne}_X := \\
\quad (\, \lambda\, f\in \mrm{Map}(X, {\bf B}). (
\text{if } f = \mrm{One}_X \text{ then } 1 \text{ else } 0 )
\,) \\
\quad \in \mrm{Map}(\mrm{Map}(X, {\bf B}), {\bf B})
`$
比喩的に言うと、$`\mrm{PickOne}`$ は、関数 $`\mrm{One}`$ だけを拾い出して〈pick up して〉、その他の関数をすべて“捨ててしまう”。「捨ててしまう」の意味は、値を $`0`$ とすること。
注意: $`\mrm{PicOne}`$ は $`\mrm{Map}(\mrm{Map}({\bf A}, {\bf B}), {\bf B})`$ の要素だから、“全員で256人のグループの特定のメンバー”(比喩)である。担当色は何かな?(ジョーク)
$`\mrm{PickOne}_{\bf A}`$ の値を全部列挙する。
- $`\mrm{PickOne}(\mrm{fun}(0, 0, 0)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(1, 0, 0)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(0, 1, 0)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(0, 0, 1)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(1, 1, 0)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(1, 0, 1)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(0, 1, 1)) = 0`$
- $`\mrm{PickOne}(\mrm{fun}(1, 1, 1)) = 1`$
$`\mrm{PickOne'}_X`$ は $`\mrm{PickOne}_X`$ とほぼ同じだが、次の図式を可換にする関数。
$`\quad \xymatrix@R+1pc@C+2pc{
{\mrm{Map}(X, {\bf B})} \ar[r]^{\mrm{PickOne'}_X}
\ar[dr]_{\mrm{PickOne}_X}
& {\mrm{Map}({\bf 1}, {\bf B})}
\\
{}
& {\bf B} \ar[u]_{\mrm{ValToPointing}}
}\\
\quad \text{commutative }\In {\bf Set}
`$
$`\mrm{PickOne'}_{\bf A}`$ の値を全部列挙する。$`\mrm{fun}(0)`$ は関数 $`(0\mapsto 0)`$ のこと。
- $`\mrm{PickOne'}(\mrm{fun}(0, 0, 0)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(1, 0, 0)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(0, 1, 0)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(0, 0, 1)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(1, 1, 0)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(1, 0, 1)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(0, 1, 1)) = \mrm{fun}(0)`$
- $`\mrm{PickOne'}(\mrm{fun}(1, 1, 1)) = \mrm{fun}(1)`$
問題 1
関数集合 $`\mrm{Map}({\bf A}, {\bf B})`$ には、8つの関数が含まれる。
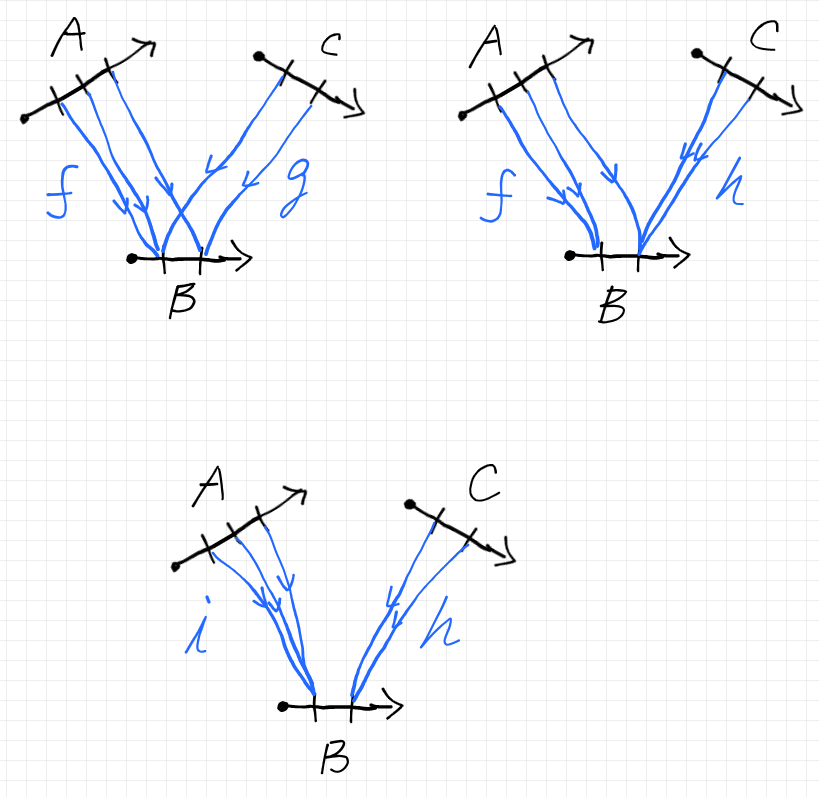
$`\quad f, g \in \mrm{Map}({\bf A}, {\bf B})`$
という前提は、「$`f, g`$ が8つの関数のどれかである」という条件を述べている。$`f, g`$ は自由に組み合わせてよいので、ペア $`(f, g)`$ は $`8\times 8 = 64`$ 個ある。その64個全体に対して、次の3つの主張は同じことを主張しているか? よくわからないなら $`f, g`$ の具体例で確認してみよ。なんなら、全数確認(64個を確認)すれば確実。
- $`f = g`$
- $`\mrm{PickOne}(f) = \mrm{PickOne}(g)`$
- $`\mrm{PickOne'}(f) = \mrm{PickOne'}(g)`$
一般に、任意の集合 $`X`$ に対して、$`f, g\in \mrm{Map}(X, {\bf B})`$ として、次の3つの主張は同じことを主張しているか?
- $`f = g`$
- $`\mrm{PickOne}_X(f) = \mrm{PickOne}_X(g)`$
- $`\mrm{PickOne'}_X(f) = \mrm{PickOne'}_X(g)`$
問題 2
関数 $`\mrm{ExcludeZero}_X`$ を次のように定義する。
$`\For X\in |{\bf Set}|\\
\Subject \mrm{ExcludeZero}_X : \mrm{Map}(X, {\bf B}) \to {\bf B} \In {\bf Set}\\
\For f \in \mrm{Map}(X, {\bf B})\\
\Define \mrm{ExcludeZero}_X(f) := \mrm{flip}(\mrm{PickOne}_X( f ; \mrm{flip} ) )
`$
$`\mrm{ExcludeZero}_{\bf A}`$ の値を全部列挙してみよ。
比喩的に言うと、$`\mrm{ExcludeZero}`$ は、関数 $`\mrm{Zero}`$ だけを“除外”して〈exclude して〉、その他の関数をすべて“拾い上げる”。「除外」の意味は、値を $`0`$ とすること。
注意: $`\mrm{ExcludeZero}`$ は $`\mrm{Map}(\mrm{Map}({\bf A}, {\bf B}), {\bf B})`$ の要素だから、“全員で256人のグループの特定のメンバー”(比喩)である。担当色は何かな?(ジョーク)
一般に、任意の集合 $`X`$ に対して、$`f, g\in \mrm{Map}(X, {\bf B})`$ として、次の2つの主張は同じことを主張しているか?
- $`f = g`$
- $`\mrm{ExcludeZero}_X(f) = \mrm{ExcludeZero}_X(g)`$
問題 3
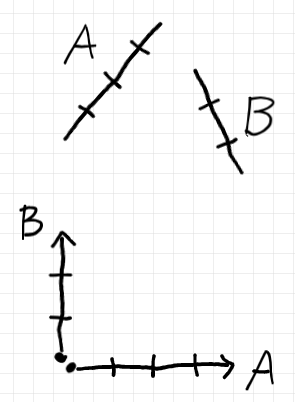
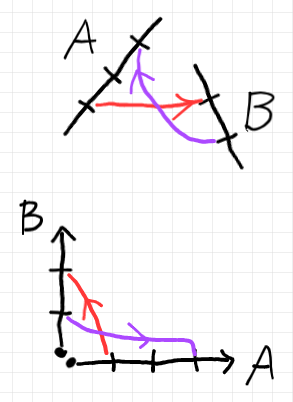
一般に、関数 $`F: S \to T \In {\bf Set}`$ があるとき、$`s, s' \in S`$ として、次の2つの主張は同じことを主張しているか?
- $`s = s' \In S`$
- $`F(s) = F(s') \In T`$
具体例として、$`S = {\bf R}, T = {\bf Z}`$ と置いて、関数 $`F: {\bf R} \to {\bf Z}`$ は実数の整数部分 $`\mrm{floor}`$ (床関数と天井関数 参照)だとして、次の2つの主張は同じことを主張しているか?
- $`s = s' \In {\bf R}`$
- $`\mrm{floor}(s) = \mrm{floor}(s') \In {\bf Z}`$
総括的に言えば:
- 「関数値が等しくなること」と「入力した引数値が等しいこと」を同じことだと思っているなら、それは誤解・誤認である。間違った認識なので修正しなくてはならない。
- 関数の学習の第一歩は、「引数値が等しい」、「関数値が等しい」、「関数が等しい」を区別して、その相互関係を理解することである。