モノイドやモノイド圏の指標 補足解説

説明 その他

参照のためにコピーした（わずかに変更）。

「マイクロコスモ原理と構造の無限タワー」に補足。記法を少し改善する。

「掛け算」「乗法」「積」などと呼ばれる演算の中置記法で使われる記号は色々ある。

  1. なし（単なる併置）
  2. ×
  3. ・
  4. \otimes
  5. 他にも色々

記号を修飾する方法は、

  1. 太字
  2. 斜体
  3. ダッシュ（プライム）
  4. 下線
  5. 上線
  6. ハット
  7. 他にも色々

色々な種類・装飾を使うのは、概念的区別をするため。これからやることは、できるだけ種類・装飾を使わないようにすること。代わりに、次元と呼ばれる番号（整数値）で識別する。

異なる次元の同じ記号を同時に使うときだけ装飾による区別が必要。僕は主に太字を使ってきたがダッシュ（'）にする。書くのが簡単。もっと重要な理由は、a, a', a'', a''' のような書き方が出来ること。“太字の太字”は、普通は出来ない。

次元nのモノ達に注目して語っている文脈で、次元(n+1)の記号が出てきたらダッシュを1つ付ける。次元(n+2)の記号にはダッシュを2つ付ける。以下同様。

これからは、「掛け算」「乗法」「積」を一律に大文字Yで表記する。Yを使う理由は象形文字としてだ。「マックレーンの五角形をインデックスなしの等式で表す」を見ればYをつかう理由がわかるだろう。

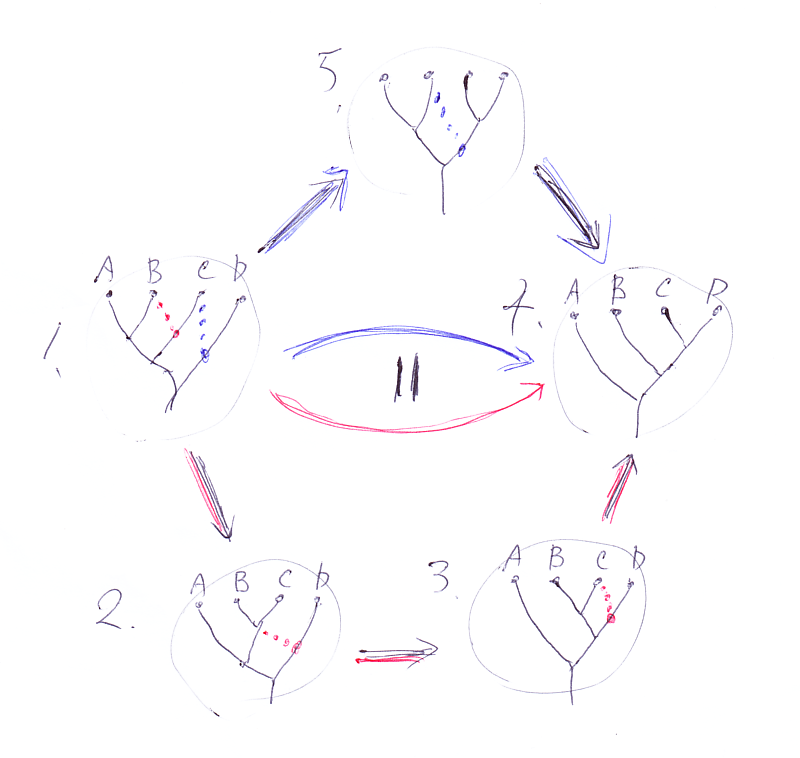
ツリー状図の合流点のイメージからY。

他に単位対象と恒等（恒等写像、恒等射、恒等関手、恒等自然変換など）を表す文字が必要だが、「マックレーンの五角形をインデックスなしの等式で表す」では 単位対象＝i, 恒等＝I としていた。象形文字としてはこれが使いやすい。

が、「マイクロコスモ原理と構造の無限タワー」では行きがかり上、単位（対象／射）をIとしている。恒等がJになっている。しかも、Iが単位対象（0-射）と単位ポインティング射（1-射）の2つの意味でオーバーロードされている。

次が、辻褄が合っていて象形文字として使いやすい。

記号 意味
U 台対象
Y 掛け算、乗法、積
1 単位対象
i 単位射
I 恒等

だがこれも、1, i, I がとても紛らわしいという欠点がある。目を凝らして注意すべし！ それと、次の点に注意しよう。

  • i:1'→U
  • i0(0) = 1 ∈ |U| （0は自明圏の唯一対象）

n次元の自明圏からのn次元の単位射（単位写像、単位関手、単位自然変換かも知れない）iの0-部分〈対象部分 | object part〉に自明対象（自明圏の唯一の0-射、自明アトム）を入れた値が(n-1)次元の単位対象。神経質に気にする必要はないが、一般に、モノイド圏や高次圏の単位の仲間（恒等、モノイド単位、ポインティング射、終対象など）は難しい → 「モノイド圏の単位対象の定義について： これ難しいやん」参照。

「マイクロコスモ原理と構造の無限タワー」に出てきた指標を、上記の象形文字に置き換えてみる。

1-signature 1-mon := {
 0-morphism U;
 1-morphism m:U\otimesU→U;
 1-morphism i:I→U;
}

\otimes → Y と置き換えたいのだが、それだと m → Y と区別がつかないので、\otimes → Y' とする。

  • U → U（変化なし）
  • m → Y
  • \otimes → 中置から前置のY'
  • i → i（変化なし）
  • I → 1'（イチ・ダッシュ）

中置から前置に切り替えるので、

  • U\otimesU → Y'(U, U)

実は、(U, U) というペアを作るためにデカルト構造が必要だったりするのだが、そこまで詮索しないことにする。（← ここが気になる人がいるのかな？ だとしたらその疑問は本質を突いている、鋭い。）

んで、書き換えると：

1-signature 1-mon := {
 0-morphism U;
 1-morphism Y:Y'(U, U)→U;
 1-morphism i:1'→U;
}

Y'と1'が１次元上からやって来ている。

次にモノイド圏の指標。

2-signature 2-mon := {
 0-morphism U;
 1-morphism Y = \otimes:U×U→U;
 1-morphism I:I→U;
 1-morphism J = IdU:U→U;
 2-morphism α::(Y×J)*Y⇒αU,U,U*(J×Y)*Y:(U×U)×U→U;
 2-morphism λ::(I×J)*Y⇒λU:I×U→U;
 2-morphism ρ::(J×I)*Y⇒ρU:U×I→U;
}

記号の種類・装飾のバラエティを取り除く。

書き換え前 書き換え後
U U
\otimes Y
× Y'
I i
I 1'
J I
* #（下添字略）
αU,U,U α'（下添字略）
λU λ'（下添字略）
ρU ρ'（下添字略） 
2-signature 2-mon := {
 0-morphism U;
 1-morphism Y: Y'(U, U)→U;
 1-morphism i:1'→U;
 1-morphism I:U→U;
 2-morphism α:: Y'(Y, I)#Y⇒α'# Y'(I, Y)#Y:  Y'(Y'(U, U), U)→U;
 2-morphism λ:: Y'(i, I)#Y⇒λ': Y'(1', U)→U;
 2-morphism ρ:: Y'(I, i)#Y⇒ρ': Y'(U, 1')→U;
}

Y', 1', α', λ', ρ' が１次元上から来ている記号。絵で描くときは：

記号 描き方
U 描かない
Y Yの形
Y' 併置のあいだの空白
i iの形かその変形
1' 点線か空白
I Iの形、ワイヤー
# 上下の併置（スタッキング）
α' ワイヤーの位置ずらし
λ' 点線（左）と実線（ワイヤー）の合流
ρ' 点線（右）と実線（ワイヤー）の合流

絵の基本は、「圏論の随伴をちゃんと抑えよう： お絵描き完全解説 - 檜山正幸のキマイラ飼育記 (はてなBlog)」とか。絵を描いてみるのはおススメ。テキスト記号だけだと、なかなか事情が分からないから。