モノイド閉圏の事例： カリー化の自然性

• 参考：ラムダ計算の自然性とお絵描き - 檜山正幸のキマイラ飼育記 (はてなBlog)

続きの記事2つあり。

内容：

記法と設定と法則

を Φ_X,A,Y に、 を □ に変える以外は元記事と同じ記号を使う。id_A などは、バンプアップ記号'^'を使って A^ などと書く。

• f:X□A→Y
• v:X'→X
• p:A'→A
• q:Y→Y'

タイトニング

• Φ_X',A,Y( (v□A^);f ) = v;Φ_X,A,Y(f) : X'→hom(A, Y)

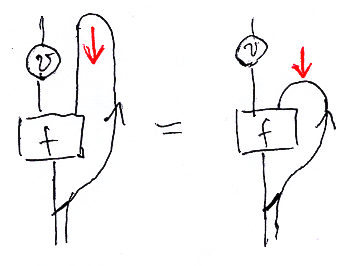
カーブに沿ったスライディング

• Φ_X,A',Y( (X^□p);f ) = Φ_X,A,Y(f);hom(p, Y) : X→hom(A', Y)

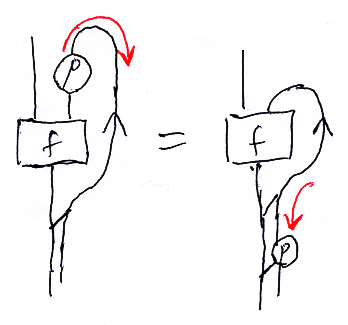
真っすぐなスライディング

• Φ_X,A,Y'( f;q ) = Φ_X,A,Y(f);hom(A, q) : X→hom(A,Y')

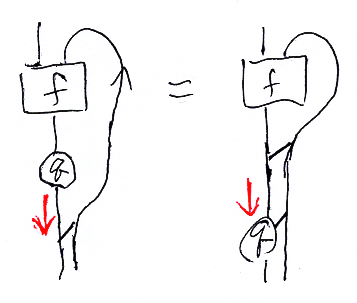
定義の確認

過去記事より、定義を引用する。

カリー化 Φ

Φ:Hom(A□B, C)→Hom(A, hom(B, C)) := λf∈Hom(A□B, C).(
  [
   λ0a∈A.(
     [
       λ0b∈B.( f(a, b) ∈C)
       ALSO
       λ1b→b'∈B.( f(a, b→b') ∈C)
     ]  ∈Hom(B, C)
   )
   ALSO
   λ1a→a'∈A.(
     [
       λ01b∈B.( f(a→a', b) ∈C)
     ] ∈Defm(B, C))
  ] ∈Hom(A, hom(B, C))
)

射のボックス積 f□g

f□g:A□C→B□D :=
[
 λ0(a, c)∈A□C.( (f(a), g(c)) ∈B□D)
 ALSO
 λ1(a→a', c)∈A□C.( (f(a→a'), g(c)) ∈B□D)
 OR
 λ1(a, c→c')∈A□C.( (f(a), g(c→c')) ∈B□D)
]

hom(p, Y), hom(A, q)

hom(p:A'→A, Y):hom(A, Y)→hom(A', Y) :=
[
  λ0u∈hom(A, Y).( p;u ∈Hom(A, Y) )
  ALSO
  λ1u⇒v∈hom(A, Y).( p;;(u⇒v) ∈Defm(A, Y) )
]

hom(A, q:Y→Y'):hom(A, Y)→hom(A, Y') :=
[
  λ0u∈hom(A, Y).( u;q ∈Hom(A, Y) )
  ALSO
  λ1u⇒v∈hom(A, Y).( (u⇒v);;q  ∈Defm(A, Y) )
]

計算

タイトニング

• Φ_X',A,Y( (v□A^);f ) = v;Φ_X,A,Y(f) : X'→hom(A, Y)

左辺 =
ΦX',A,Y( (v□A^);f :X'□A→Y) : X'→hom(A, Y) =
[
 λ0x'∈X'.(
   [
     λ0a∈A.( ( (v□A^);f)(x', a) ∈Y)
     ALSO
     λ1a→a'∈A.( ( (v□A^);f)(x', a→a') ∈Y)
   ]  ∈Hom(A, Y)
 )
 ALSO
 λ1x'→x''∈X'.(
   [
     λ01a∈A.( ( (v□A^);f)(x'→x'', a) ∈Y)
   ] ∈Defm(A, Y))
] : X'→hom(A, Y)
=
[
 λ0x'∈X'.(
   [
     λ0a∈A.( f(v(x'), a) ∈Y)
     ALSO
     λ1a→a'∈A.( f(v(x'), a→a') ∈Y)
   ]  ∈Hom(A, Y)
 )
 ALSO
 λ1x'→x''∈X'.(
   [
     λ01a∈A.( f(v(x'→x''), a) ∈Y)
   ] ∈Defm(A, Y))
] : X'→hom(A, Y)

右辺 = v;Φ_X,A,Y(f:X□A→Y) :X'→hom(A, Y) を計算するにあたって、Φ_X,A,Y(f:X□A→Y) = Φ(f) = F :X→hom(A, Y) と置く。すると、

• 右辺 = v;F :X'→hom(A, Y)

後半の（α, β, ... とは違う）ギリシャ文字小文字をブロック変数として使う。ブロック変数は説明してないが見当は付くだろう。

  v;F
= v;(λξ∈X.F(ξ))
= λξ'∈X'./( F(ξ) / ξ = v(ξ') )/

これに対して、次の定義を使う。

F = 
   [
   λ0x∈X.(
     [
       λ0a∈A.( f(x, a) ∈Y)
       ALSO
       λ1a→a'∈A.( f(x, a→a') ∈Y)
     ]  ∈Hom(A, Y)
   )
   ALSO
   λ1t→t'∈X.( /* 都合により変数名は t */
     [
       λ01a∈A.( f(t→t', a) ∈Y)
     ] ∈Defm(A, Y))
  ] : X→hom(A, Y)

右辺
= v;F
= v;(λξ∈X.F(ξ))
= λξ'∈X'./(
  F(ξ)
  /
  ξ = v(ξ')
)/
=
λ{x' ALSO x'→x''}∈X'./(
   [
   λ0x∈X.(
     [
       λ0a∈A.( f(x, a) ∈Y)
       ALSO
       λ1a→a'∈A.( f(x, a→a') ∈Y)
     ]  ∈Hom(A, Y)
   )
   ALSO
   λ1t→t'∈X.( /* 都合により変数名は t */
     [
       λ01a∈A.( f(t→t', a) ∈Y)
     ] ∈Defm(A, Y))
  ]
  /
  {x ALSO t→t'} = v({x' ALSO x'→x''})
)/
=
λ{x' ALSO x'→x''}∈X'.(
   {
     [
       λ0a∈A.( f(v(x'), a) ∈Y)
       ALSO
       λ1a→a'∈A.( f(v(x'), a→a') ∈Y)
     ]  ∈Hom(A, Y)
   ALSO
     [
       λ01a∈A.( f(v(x'→x''), a) ∈Y)
     ] ∈Defm(A, Y)
  }
)
=
[
 λ0x'∈X'.(
   [
     λ0a∈A.( f(v(x'), a) ∈Y)
     ALSO
     λ1a→a'∈A.( f(v(x'), a→a') ∈Y)
   ]  ∈Hom(A, Y)
 )
 ALSO
 λ1x'→x''∈X'.(
   [
     λ01a∈A.( f(v(x'→x''), a) ∈Y)
   ] ∈Defm(A, Y))
] :X'→hom(A, Y)

念のため、最後の式をコピーして比較。

左辺 = 
[
 λ0x'∈X'.(
   [
     λ0a∈A.( f(v(x'), a) ∈Y)
     ALSO
     λ1a→a'∈A.( f(v(x'), a→a') ∈Y)
   ]  ∈Hom(A, Y)
 )
 ALSO
 λ1x'→x''∈X'.(
   [
     λ01a∈A.( f(v(x'→x''), a) ∈Y)
   ] ∈Defm(A, Y))
] : X'→hom(A, Y)

右辺 =
[
 λ0x'∈X'.(
   [
     λ0a∈A.( f(v(x'), a) ∈Y)
     ALSO
     λ1a→a'∈A.( f(v(x'), a→a') ∈Y)
   ]  ∈Hom(A, Y)
 )
 ALSO
 λ1x'→x''∈X'.(
   [
     λ01a∈A.( f(v(x'→x''), a) ∈Y)
   ] ∈Defm(A, Y))
] :X'→hom(A, Y)

続きは別記事。