※この記事は「記事8」
証明図が描けるようになることは目的にしてないが、特定の典型的例については理解しておいたほうが良いと思うので、2020年2月2日に出した図の詳しい解説をする。例題の図を頑張って丹念に追いかければ、形式化された推論・証明に対して、かなり具体的なイメージを持てるだろう。
演繹システムが行う証明行為とは、データ(主に入れ子のツリー構造)を順番に加工することである。各ステップごとの基本的なデータ加工は、完全に機械的・アルゴリズム的なものである。ステップを積み重ねた全体もまた機械的・アルゴリズム的な行為になる。
演繹システムの(証明成功時の)出力とは、一連のデータ加工のログ〈記録 | 履歴〉である。ユーザーである人間(または他のシステム)は、ログを追いかけて、実行されたデータ加工操作が前もって許されたもの(組み込み、またはユーザーが追加したもの)であるかどうかをチェックできる。
人間でもチェック可能とするには、グラフィカルな分かりやすい表示が必要になる。が、組版・印刷の制約から、十分にグラフィカルにはなってない。極端に省略されたテキストで表現されるのが普通である。
内容:
記法の約束
2020年2月2日に口頭で述べた(愚痴った)ように、「含意'⇒', 伴意'→'」はマズかったかも、と思うけど、「含意'⇒'」を今更変更するのもナンだから、次の約束をする。
- 1階のシーケントの矢印〈1階の伴意記号〉は、'-->'(マイナス・マイナス・大なり)にする。
- 2階のシーケントの矢印〈2階の伴意記号〉は、'==>'(イコール・イコール・大なり)にする。
'⇒' と '==>' はだいぶ紛らわしいが、注意すれば区別できるだろう。
'⇒'、'-->'、'==>' は、いずれも形式化された表現内で使う記号だが、内容的な意味は次のとおり。
- A⇒B : ¬A∨B と同じ。'⇒'は、短く書くための略記用記号だと思えばよい。
- A1, ..., An --> B : いくつかの論理式 A1, ..., An を仮定すると、 論理式 B を(結論として)推論できる/できた。
- K1, ..., Kn ==> J : いくつかの1階の推論 K1, ..., Kn を認めるなら、1階の推論 J を“推論”できる/できた。
「“推論”」と書いた部分は「2階の推論」のことで、「正しいと認める推論から、正しいと認める推論を導く」規則のこと。これも紛らわしく誤解が生じやすいので、次の約束をする。
- 単に「推論」と言ったら「1階の推論」のこと。
- 「2階の推論」は「リーズニング」と呼ぶ。
- 「推論=1階の推論」の図を積み重ねた図は証明図
- 「リーズニング=2階の推論」の図を積み重ねた図はリーズニング図
推論〈inference〉と証明〈proof〉の差はあまりない。システム組み込みで、それ以上は(当該システム内では)分解できない証明を「推論」と呼ぶ習慣があるだけ。「推論」の代わりに「組み込み証明」とか「基本証明」とか言ってもよい、つうか、そのほうが整合的。また、必ずしも「組み込み」「基本」でない証明を「推論」と呼ぶこともあるので注意(習慣はとにかくイイカゲンだからね)。
| 基本的な証明 | 基本とは限らない証明 | |
|---|---|---|
| 1階の | 推論, 基本証明 | (原則的には)証明 |
| 2階の | 基本リーズニング | リーズニング |
「(原則的には)証明」と書いたのは、「推論」と「証明」の区別をたいしてしないこともあるから。
'-->'、'==>' は、本来はメタ記号(メタな記述に使われる記号)ではないのだが、メタ記号に流用されてしまうことが多いし、まー、形式化/メタの境界を曖昧にしてイイカゲンに書くのは便利だったりもする(苦笑)。
- 論理式単位で入出力・処理するシステム S における証明可能性 A1, ..., An |-S B を、A1, ..., An --> B と書くことがある。
- シーケント単位で入出力・処理するシステム S' における証明可能性 X1, ..., Xn |-S' Y (X1, ..., Xn, Y は1階のシーケント)を X1, ..., Xn ==> Y と書くことがある。
普通の論理記号('∧'とか'∀')でさえ、形式化された記号とメタな記号を区別しない人が多い現状だから、これは致し方ない。文脈により、形式化されているか、メタかを判断する。
形式化された記号とメタな記号の区別を、見た目ですることは無理がある。違いは使い方にあるから。
- システムへの入力、システムからの出力、システムの内部処理データに使われる記号は形式化された記号である。
- 人間と人間のコミュニケーションのために、自然言語に混ぜて使われる記号はメタな記号である。
つまり、記号そのものに「形式化/メタ」〈formalized/meta〉の区別があるのではなくて、使う状況で「形式化された記号として使う/メタな記号として使う」の区別が生じる。
例題
Sは、シーケントを入出力と内部データに使う演繹システムとする。単独の論理式 A は入力に使えず、代わりにシーケント T --> A を使うとする。シーケントが形式化された表現であることを強調する目的で "T --> A" のように引用符で囲む(必要があれば、だが)。
- "A∧B --> C" |-S "T --> A⇒(B⇒C)"
これはメタな記述。まったく同じことを日本語で書き直すなら:
- シーケント"A∧B --> C"を、事前に(前提として)システムSに記憶させた状態で、シーケント"T --> A⇒(B⇒C)"をターゲット(証明すべきシーケント)として入力すると、Sはターゲットをちゃんと証明する/した。
「ちゃんと証明した」とは、証拠となる証明図(人間が解釈可能なグラフィカルデータ)を出力したこと。シーケントベースのシステムは2階の証明図、すなわちリーズニング図を出力する。そのリーズニング図は次のよう。図が小さいが、後で拡大図を載せる(スマホだと拡大しても厳しいかも)。
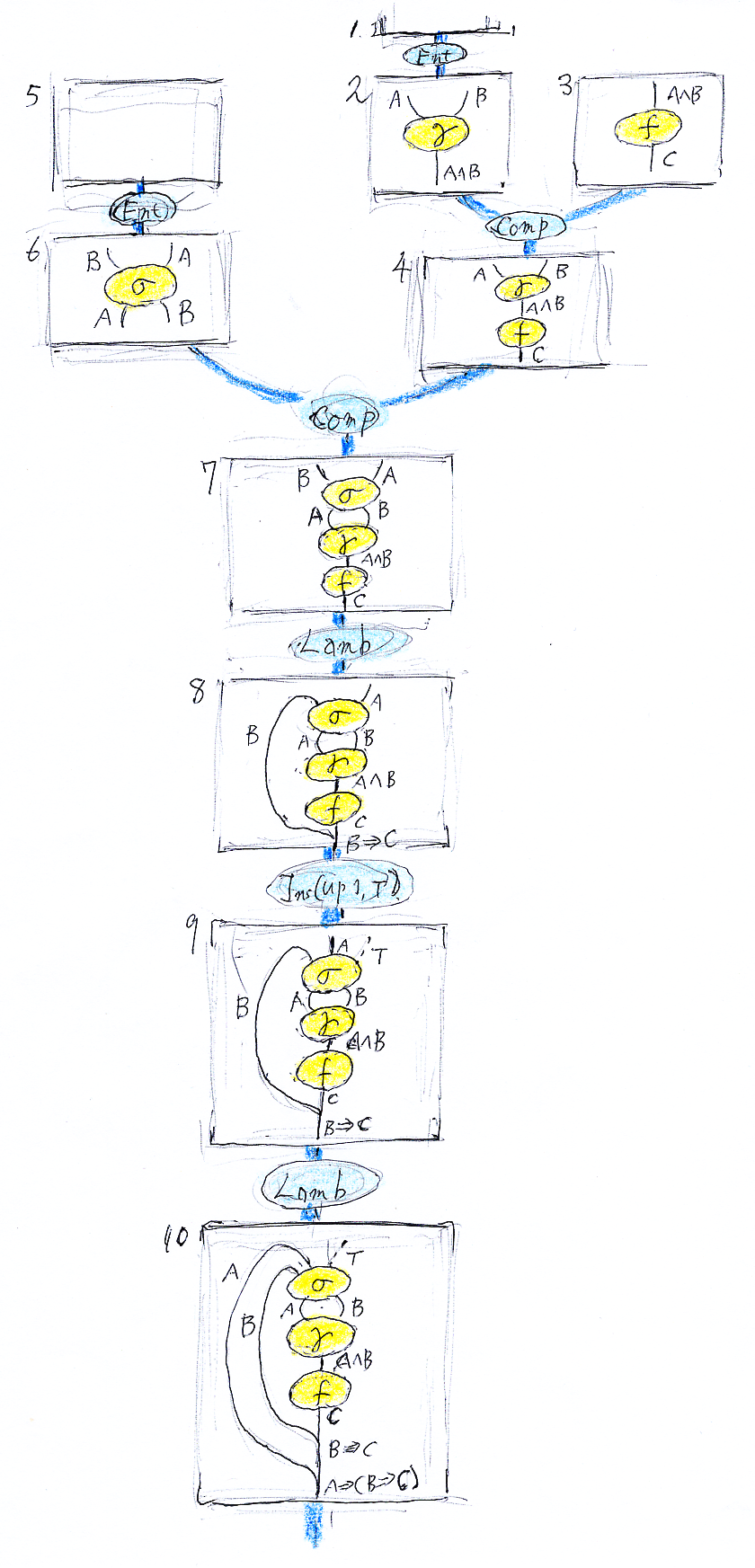
システムSが組み込みで持っている推論(1階の推論)で、図に現れるのは次のとおり(2つだけ)。
A B ------ σ(並び順の交換) B A A B ------ γ(連言導入) A∧B
事前に、ユーザーが入力した推論は次。
A∧B ------ f C
それぞれを、名前付きシーケント(名前は左端、名前の後にコロン)で書けば:
- σ:A, B --> B, A
- γ:A, B --> A∧B
- f:A∧B --> C
縦書きの推論図、横書きのシーケント、そしてグラフィカルな図は、完全に同じ内容を違う表現法で表したものである。内容的にはまったく同じ!
σとγには、A, B を添字で付けるのがより正確である。
- σA,B:A, B --> B, A
- γA,B:A, B --> A∧B
また、σA,B:A, B --> B, A における右辺のカンマは、ゲンツェンのLKとは解釈が違う。右辺のカンマも連言〈and〉と解釈する。
[/補足]
基本リーズニングの規則と図
システムが組み込みで持っている基本リーズニング規則〈2階の推論規則〉で、例題の図に登場するのは次のとおり。
- Ent〈Enter | 登場 〉 : 何もない状態から、組み込みの証明図〈推論図〉を出現させる。
- Comp〈Composition | 結合〉: 2つの(1階の)証明図を上下にくっつける。
- Lamb〈Lambda〉 : 証明図の最上段の論理式を、最下段に移動して、含意の前件にする。ラムダ計算のラムダ抽象に相当するのでLambda。演繹原理を実現するための操作とも言える。
- Ins〈Insert〉 : 証明図の指定された位置に論理式を挿入する。
これらの基本リーズニングを、シーケントと縦書きのテキストで表現すれば:
☆ ===========Ent Γ --> A Γ --> Δ Δ --> B =====================Comp Γ --> B A, Γ --> B =============Lamb Γ --> A⇒B Γ --> A =============Ins[up, 0, T] T, Γ --> A
説明:
- '☆'は「何もない」ことを表す。空な証明図。
- Γは論理式のリスト
- Insに付いている'up'は最上段の証明図の上側を意味し、0 は左端の位置を示す。最初の論理式の右の位置なら 1。
グラフィカルな表現とテキスト表現
メタな命題 "A∧B --> C" |-S "T --> A⇒(B⇒C)" の証拠となるグラフィカルなリーズニング図〈2階の証明図〉は次(今度は大きい)。

6,4,7,8 の部分だけテキストで書いてみる。
B A A B
-----σ -------γ
A B A∧B
----- f
C
=====================Comp
B A
-----σ
A B
-----γ
A∧B
----- f
C
========Lamb
[B] A
-----σ
A B
-----γ
A∧B
----- f
C
-----
B⇒C
説明:
- [B] は、移動した跡を示す。実際には、ここにあった B は、最下段の含意前件(左側)に移動している。Lambの効果をリアルに再現するには、Bをホントに移動して見せるアニメーションが適切。
[追記]
試しに、上の縦書きリーズニング図で出てくる最初の Comp を横書きしてみる。
σ:B,A→A,B
Comp:: ==> σ:B,A→A,B; γ:A,B→A∧B; f:A∧B→C
γ:A,B→A∧B; f:A∧B→C
Comp操作の上段の左右を右側の上下に、Compの入出力の上下配置を左右配置に変更した。さらに、左側の上下も左右に潰すと:
Comp::(σ:B,A→A,B), (γ:A,B→A∧B; f:A∧B→C) ==> σ:B,A→A,B; γ:A,B→A∧B; f:A∧B→C
単に、書き方における 上下←→左右 の入れ替えに過ぎない。こういうクダラナイとも言える書き方のドタバタに付き合わされるのはバカバカしいのだが、組版・印刷というユーザーインターフェースの制約内での伝達の苦労と工夫の結果。現状では、このテの苦労と工夫に付き合って、書き換え練習をするしかない。
[/追記]
全部をテキストで書くのは大変なので、1階の証明図の仮定と結論だけ抜き出してシーケントにすると:
B, A --> A, B A, B --> C =============================Comp B, A --> C ============Lamb A --> B⇒C
格段に短くなる。さらに、横線を二重線(イコールの繰り返し)で書くのもやめて、リーズニングの名前も省略:
B, A --> A, B A, B --> C ----------------------------- B, A --> C ------------ A --> B⇒C
実際に使われるのはこの形。生の正確なログ〈記録 | 履歴〉は膨大になるので、省略に省略を重ねてコンパクトに書くようにしている。
縦書きの証明図の仮定と結論を横書きにするのに '-->' を使ったのと同様に、上記の縦書きリーズニング図〈2階の証明図〉の仮定(上段のシーケント)と結論(下段のシーケント)を抜き出して横書きにするのに '==>' を使えば:
- (B, A --> A, B), (A, B --> C) ==> (A --> B⇒C)
このような2階のシーケントをデータとして加工する演繹システムもあるが、古典論理の形式的証明では、1階のシーケントの加工で間に合う。
実際に使われる表現・表示の方法
例題のグラフィカル表現のような絵を描くのは僕(檜山)くらいで、ほとんど誰も描かない。実際に使われる表現・表示の方法は:
- 最後の証明図、例でいえば 10 の証明図だけを提示する。
- 前節で述べた方法でシーケントの証明図を提示する。
10 の証明図だけを提示(使った規則は省略):
T [B] [A] ------- A B ------ A∧B ------ C ------ B⇒C ---------- A⇒(B⇒C)
シーケントの証明図を提示:
☆
----------------
☆ A, B --> A∧B A∧B --> C
------------ ---------------------------
B, A --> A, B A,B --> C
----------------------------
B, A --> C
--------------
A --> B⇒C
--------------
A,T --> B⇒C
-----------------
T --> A⇒(B⇒C)
慣れれば、省略されている様々な情報を自力で補完できるが、あまりにも省略し過ぎだと思いませんか?