※ この記事は、清書して「ストリング図と相性が良いテンソル計算 2/2」の続きの記事にするかもしれない(しないかも知れない)。
テンソル計算のストリング図で次のように輪〈ループ〉を作ると、それはトレース〈対角和〉になる。$`\newcommand{\I}{\mathrm{I}}
\newcommand{\C}{\mathop{;}}
\newcommand{\Idx}[2]{ {\scriptsize \begin{pmatrix} #1 \\ \downarrow\\ #2\end{pmatrix} } }
\require{color}
\newcommand{\di}[1]{\textcolor{orange}{#1} } % dummy index
%`$
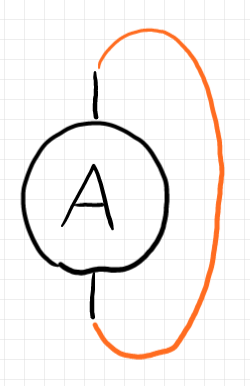
納得がいかないのであれば、次の図を考える。
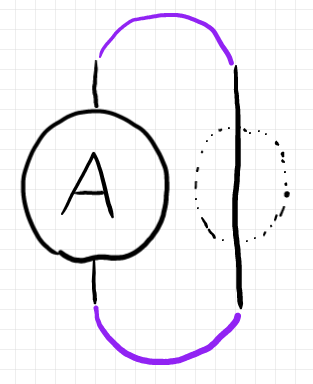
こっちは、一気にクルリンと輪を作るのではなくて、$`A`$ と恒等(象形文字で $`\I`$)とのテンソル積を作って、上下に $`\wedge, \vee`$ (紫色)を結合する。全体は:
$`\quad \wedge \C (A \otimes \I)\C \vee`$
$`\wedge, \I, \vee`$ の成分表示は「ワイヤーベンディングと条件化オペレーター」にも書いてあるが:
$`
\quad \wedge\Idx{*}{i, j} = \delta(i, j)\\
\quad \I\Idx{j}{j'} = \delta(j, j')\\
\quad \vee\Idx{i', j'}{*} = \delta(i', j')
`$
簡単な具体例としては、$`i, j, i', j' \in \{1, 2\}`$ を想定すればいい。
$`\quad ( \wedge \C (A \otimes \I)\C \vee )\Idx{*}{*}\\
= \\
\quad \wedge\Idx{*}{\di{i}, \di{j}}\\
\quad A\Idx{\di{i}}{\di{i'}} \I\Idx{\di{j}}{\di{j'}}\\
\quad \vee\Idx{\di{i'}, \di{j'}}{*}\\
`$
横一行書きにすれば:
$`\quad
\wedge\Idx{*}{\di{i}, \di{j}}
A\Idx{\di{i}}{\di{i'}} \I\Idx{\di{j}}{\di{j'}}
\vee\Idx{\di{i'}, \di{j'}}{*}
`$
省略していた総和記号をちゃんと書けば:
$`\quad \sum_{i, j, i', j'}
\wedge\Idx{*}{i, j}
A\Idx{i}{i'} \I\Idx{j}{j'}
\vee\Idx{i', j'}{*}
`$
直感的にピンとこない/納得できないのであれば、クソバカ丁寧計算で確認するしかない。
以下、クソバカ丁寧計算:
$`\quad \sum_{i, j, i', j'}\wedge\Idx{*}{i, j}A\Idx{i}{i'} \I\Idx{j}{j'}\vee\Idx{i', j'}{*}\\
= \sum_{i, j, i', j'}\delta(i, j)A\Idx{i}{i'}\delta(j, j')\delta(i', j')\\
= \sum_{i, j, i'}\sum_{j'} \delta_j(j') \delta(i, j)A\Idx{i}{i'}\delta(i', j')\\
= \sum_{i, j, i'} \delta(i, j)A\Idx{i}{i'}\delta(i', j)\\
= \sum_{i, j}\sum_{i'} \delta_j(i') \delta(i, j)A\Idx{i}{i'}\\
= \sum_{i, j} \delta(i, j)A\Idx{i}{j}\\
= \sum_{i}\sum_{j} \delta_i(j) A\Idx{i}{j}\\
= \sum_{i} A\Idx{i}{i}\\
= \mathrm{tr}(A)
`$
総和記号を省略したままで計算するなら以下。クロネッカーのデルタでインデックスがリネームされることは「ストリング図と相性が良いテンソル計算 2/2」の「恒等、コピー、スワップ」参照。
$`\quad \wedge\Idx{*}{\di{i}, \di{j}} A\Idx{\di{i}}{\di{i'}} \I\Idx{\di{j}}{\di{j'}} \vee\Idx{\di{i'}, \di{j'}}{*}\\
= \delta( \di{i}, \di{j} ) A\Idx{\di{i}}{\di{i'}} \delta(\di{j}, \di{j'})\delta(\di{i'}, \di{j'}) \\
= \delta( \di{i}, \di{j} ) A\Idx{\di{i}}{\di{j'}} \delta(\di{j}, \di{j'}) \\
= \delta( \di{i}, \di{j} ) A\Idx{\di{i}}{\di{j}} \\
= A\Idx{\di{i}}{\di{i}} \\
= \mathrm{tr}(A)
`$
文字のリネームはどんな順序でもいいので、以下でもかまわない。
$`\quad \wedge\Idx{*}{\di{i}, \di{j}} A\Idx{\di{i}}{\di{i'}} \I\Idx{\di{j}}{\di{j'}} \vee\Idx{\di{i'}, \di{j'}}{*}\\
= \delta( \di{i}, \di{j} ) A\Idx{\di{i}}{\di{i'}} \delta(\di{j}, \di{j'}) \delta(\di{i'}, \di{j'})\\
= A\Idx{\di{j}}{\di{i'}} \delta(\di{j}, \di{j'}) \delta(\di{i'}, \di{j'})\\
= A\Idx{\di{j'}}{\di{i'}} \delta(\di{i'}, \di{j'})\\
= A\Idx{\di{j'}}{\di{j'}}\\
= \mathrm{tr}(A)
`$
いざとなったら、計算が出来ることが重要。 直感的にピンとくる場合もそうでない場合も、信頼できる事実は計算と証明で支えられているのだから。
インデックスが、記号 $`i, j`$ 等で具体性に欠けるのなら、$`i, j, i', j' \in \{1, 2\}`$ として、全部具体的番号で成分列挙して、総和記号も足し算に展開して、といった超泥臭い計算をすれば実感は湧くはず。例えば:
$`\quad \delta( \di{i}, \di{j} ) A\Idx{\di{i}}{\di{j}} \\
= \sum_{i,j}\delta( i, j ) A\Idx{i}{j} \\
= \delta( 1, 1 ) A\Idx{1}{1} + \delta(1 , 2 ) A\Idx{1}{2} + \delta(2 , 1 ) A\Idx{2}{1} + \delta( 2, 2 ) A\Idx{2}{2} \\
= 1 A\Idx{1}{1} + 0 A\Idx{1}{2} + 0 A\Idx{2}{1} + 1 A\Idx{2}{2} \\
= A\Idx{1}{1} + A\Idx{2}{2} \\
= \sum_{i}A\Idx{i}{i} \\
= A\Idx{\di{i}}{\di{i}} \\
= \mathrm{tr}(A)
`$
完全なストランド図をそれなりに精密に頑張って描くとかも効果がある。[追記]「トレースを絵に描く」参照[/追記]
- actually get your hands dirty.