(仮名)アルファさんの発想が面白い。本人のなかでは一貫している(飛躍がない)のかも知れない。「教わったとおりにやった」だけかも知れない。檜山が言ったであろうこと(あまり憶えてないが絶対言いそう):
- 無限集合は難しいから最初は有限集合で考えたほうがいい。
- 関数に固執しないで、関係の特別なものと捉えなさい。
- 入出力の向きも(必要になるまで)気にしないでいい。行列・関係の転置はいつでもできる。
- 関係(実体は部分集合)は「そこに居るだけ」で、動作は伴わない。“対応”として使いたいなら、自分で目線移動しなさい。
- 特定のメンタルモデルに固執しない。
- 比喩はあくまで比喩だから、まに受けない。
- 整合性があるなら、書き方や描き方はなんでもいい。世間の習慣など無視して自由に考えてよい。
例題
例として、
- $`A = \{a_1, a_2, a_3\}`$
- $`B = \{b_1, b_2\}`$
- $`C = \{c_1, c_2\}`$
として、$`f, g`$ は以下のとおり。
- $`f(a_1) = b_2`$
- $`f(a_3) = b_1`$
- $`g(b_2) = c_2`$
$`f, g`$ はたまたま部分関数だが、任意の関係〈非決定性関数〉でよい。$`f, g`$ は次のブール係数行列で表現できる。
$`\quad \begin{bmatrix}
0 & 0 & 1 \\
1 & 0 & 0
\end{bmatrix}
`$
$`\quad \begin{bmatrix}
0 & 0 \\
0 & 1
\end{bmatrix}
`$
アルファさんの最初の提案
檜山は下図の左のような説明をした。赤は $`f`$ 、青は $`g`$ を表す。目線移動を特に強調したわけでもないが、アルファさんは目線移動の線(赤線と青線)を意識していたのかも知れない。
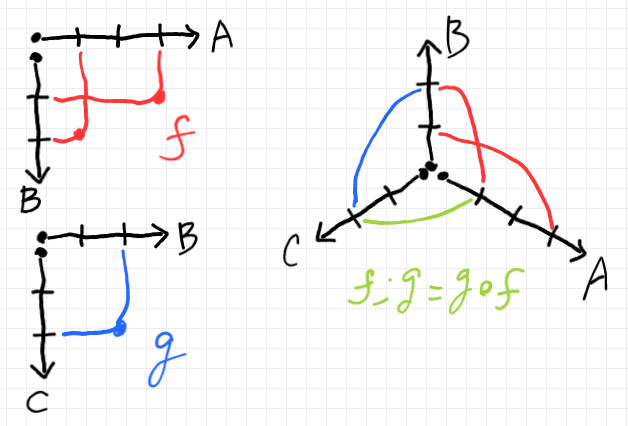
$`f`$ の絵と $`g`$ の絵が離れているのがイヤ、目線移動がスムーズにいかないのがイヤ、という理由で、上図の左のような描画法をアルファさんが提案。この時点では、まだマス目にそった(直角に曲がる)目線移動だったかも知れない。
$`f`$ と $`g`$ の結合 $`f;g = g\circ f`$ は、ショートカット(回り道しないで直接行く)緑の線で表現できる。が、「入出力の向きも(必要になるまで)気にしないでいい。」と檜山に言われているので、向き=矢印はあまり意識してない(おそらく)。
アルファさんの次の提案
下図の下段の右側がアルファさんの次の提案。
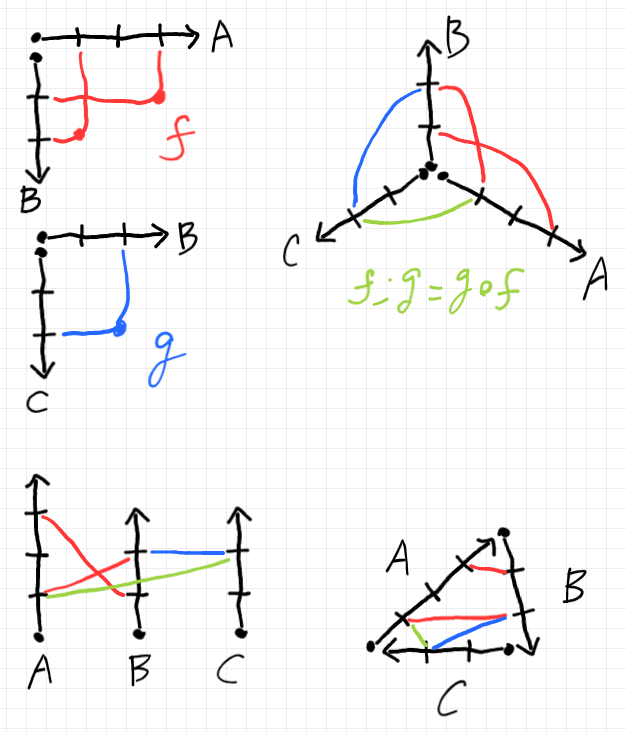
下段左側は檜山が教えたストランド(棒や紐〉による図法。そこから下段右側に至る発想は(おそらく):
- 上段左側の4本の“座標軸”を、上段右側にするとき、“座標軸”をまとめたり方向を変えたりの“再配置”をしている。
- 上段右側と下段左側も、“座標軸”を“再配置”しているに過ぎない。
- だったら、“座標軸”をどう“再配置”するのも自由だ。「書き方や描き方はなんでもいい。世間の習慣など無視して自由に考えてよい。」と檜山が言っていた。
- “座標軸”を外側の三角形にしたら見やすい。
- 「比喩はあくまで比喩」と檜山が言っていたから、ホントの3次元空間にこだわる必要はない。“座標軸”が5,6本あっても同じように描ける。
さらには、描画経験から自然に次のような認識も得ている。
- 抽象的多次元空間の一点は、多角形で表現できる。
- 抽象的多次元空間内の部分集合は、多角形の集まり。有限集合なら、幾つかの多角形を重ね書きして具体的に描ける。
- 抽象的多次元空間内の部分集合は、必ずしも関数や関係のグラフと考える必要はない。考えたいなら、グラフと考えてもよい。自由だ。
- 多角形(多次元空間の一点)が与えられれば、対応を取り出すことはできる。例えば、三角形の一辺から向かい合う頂点を決めるように。
- 多角形の幾つかの頂点から作られる小さい多角形(ときに辺や頂点)は、点を射影したモノになる。例えば、三角形の辺は座標平面への射影、三角形の頂点は座標軸〈座標直線〉への射影。もちろん、「平面」や「座標軸」は比喩だから「まに受けない。」(と、檜山が言っていた。)