有限集合だけを考える。
- $`A = \{a_1, a_2, a_3\}`$
- $`B = \{b_1, b_2\}`$
- $`C = \{c_1, c_2\}`$
$`A`$ を次のように描く、$`B, C`$ も同様。
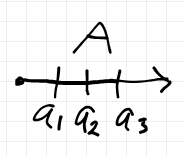
- 関数も関係も集合だと思えば列挙可能。有限集合の世界では、あらゆるものが具体的に列挙可能。
- 関数は逆関数が作れないときがあるが、関係だと思えば転置は常に可能。
- 直積、ファイバー積、関係の結合〈composition〉、ジョインも列挙可能。
- ファイバー積と結合では中間情報は捨てる。ジョインは中間情報も残す。
書き出すときに面倒なら、$`A, B, C \subseteq {\bf N}`$ と考えてしまってもかまわない。それなら:
- $`A = \{1, 2, 3\}`$
- $`B = \{1, 2\}`$
- $`C = \{1, 2\}`$
記法
ここの $`f, g`$ は一般名。
- $`\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }A\NFProd{f}{B}{g}C`$ ファイバー積、$`B`$ の情報を捨てる。
- $`\newcommand{\NJoin}[3]{ \mathop{_{#1} \!\underset{#2}{\Join}\,\!_{#3} } } A\NJoin{f}{B}{g}C`$ ジョイン、$`B`$ の情報を残す。
- $`f;g`$ 関係の結合、関数も関係の一種とみなす。
- $`f^t`$ 関係の転置、関数も関係の一種とみなす。
- $`A\times C`$ 単なる直積
設定
ここから先、$`f, g,h,i`$ は固有名。
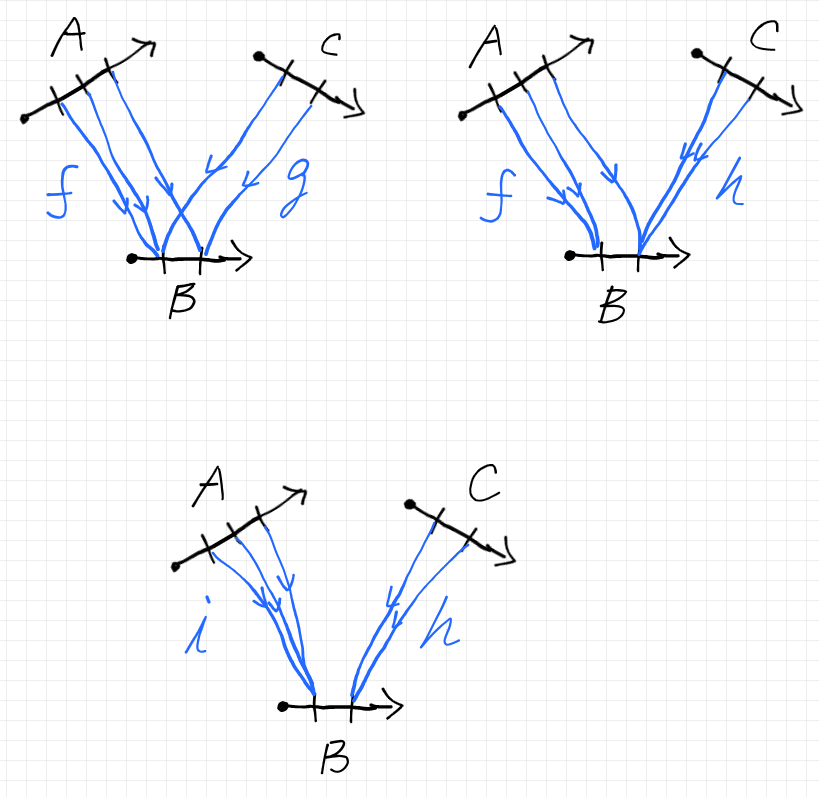
プロファイル
- $`f\subseteq A\times B`$ つまり $`f \in {\bf UTens}(A, B) = \mathrm{Pow}(A\times B)`$
- $`g\subseteq C\times B`$
- $`h\subseteq C\times B`$
- $`i\subseteq A\times B`$
- $`A\NFProd{f}{B}{g}C \subseteq A\times C`$
- $`A\NJoin{f}{B}{g}C \subseteq A\times B \times C`$
- $`f; g^t \subseteq A\times C`$
- $`g; f^t \subseteq C\times A`$
- $`A\NFProd{f}{B}{h}C \subseteq A\times C`$
- $`A\NJoin{f}{B}{h}C \subseteq A\times B \times C`$
- $`f; h^t \subseteq A\times C`$
- $`h; f^t \subseteq C\times A`$
- $`A\NFProd{i}{B}{h}C \subseteq A\times C`$
- $`A\NJoin{i}{B}{h}C \subseteq A\times B \times C`$
- $`i; h^t \subseteq A\times C`$
- $`h; i^t \subseteq C\times A`$
問題 1
要素をすべて列挙せよ。
- $`f`$
- $`g`$
- $`h`$
- $`i`$
- $`A\NFProd{f}{B}{g}C`$
- $`A\NJoin{f}{B}{g}C`$
- $`f; g^t`$
- $`g; f^t`$
- $`A\NFProd{f}{B}{h}C`$
- $`A\NJoin{f}{B}{h}C`$
- $`f; h^t`$
- $`h; f^t`$
- $`A\NFProd{i}{B}{h}C`$
- $`A\NJoin{i}{B}{h}C`$
- $`i; h^t`$
- $`h; i^t`$
問題 2
要素をすべて列挙せよ。
- $`A\times C`$
- $`A\times B \times C`$
- $`A\NFProd{!_A}{\bf 1}{!_C}C`$
- $`A\NJoin{!_A}{\bf 1}{!_C}C`$
問題 3
問題1で列挙した結果を眺めて、次の一般的定理が成立することを確認せよ。以下で出てくる名前は、今までの固有名ではなくて、一般論における一般的定理を記述する一般名。例えば、$`A`$ は一般的になんらかの集合であって、三元集合とは限らない(老婆心で注意)。
- $`A\NFProd{f}{B}{g}C \cong f;g^t`$ (イコールだとしても、それを $`\cong`$ と書いて悪いわけではない。)
- $`(A\NFProd{f}{B}{g}C)^t \cong g;f^t`$
- $`A\NFProd{f}{B}{g}C \cong \sum_{b \in B}(f^{-1}(b) \times g^{-1}(b))`$
- $`(A\NFProd{f}{B}{g}C)^t \cong \sum_{b \in B}(g^{-1}(b) \times f^{-1}(b))`$