(仮名)アルファさんの図法は、ちょっと衝撃的だった。「こだわりのなさ」に驚いた。アルファ図法のアイディアをまとめておく。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{\text{-} }
`$
内容:
座標軸と点
原則として、有限集合とその直積を考える。話は無限集合でも通用するが、アルファさん自身は無限集合を考えてない。
- 線分で有限集合を表す。ただし、線分自体は“入れ物/置き場所”に過ぎない。
- 有限集合の要素は、線分上の“目盛り”で表す。
- “目盛り”がない線分は空集合を表す。
- 線分の飾りや向き・位置などは何でもいい(これ重要)。
“座標軸”っぽい飾りを付けてもいいが、飾りはなくてもいい。例として次の集合を考える。
- $`A = \{a_1, a_2, a_3\}`$
- $`B = \{b_1, b_2\}`$
「集合 $`A`$ と集合 $`B`$ があります」という状況を描画するには、下図の上段でも下段でも本質的な差はない、どうでもいい、ということになる。
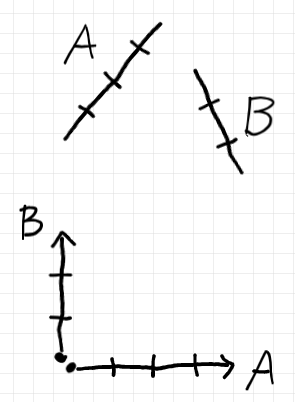
ここで、アルファ図法のテクニカルタームを導入する。テクニカルタームなので、国語辞書的意味や既存の他の意味にこだわらないでそのまま素直に受け入れる。(「こだわらない」「素直に」がアルファさんのアイディアの源泉のようだ。)
- 座標軸: 集合を表す線分
- (座標軸上の)点: 集合の要素を表す座標軸の目盛り刻み
テキスト記法
$`R`$ が直積集合(例えば、$`A\times B`$)の部分集合で、$`x`$ が $`R`$ の要素であることを次のように書く。
$`\quad x \in R \subseteq A\times B`$
$`R`$ を「$`A`$ から $`B`$ への関係」とみなす場合は次のように書く。
$`\quad R : A \to B \In {\bf Rel}`$
$`(a, b)\in R`$ は、$`R`$ を関係とみなすと次の意味だ。
- $`R`$ により、$`a\in A`$ は $`b\in B`$ と対応している。
これを次のように書く。関数による対応ではないので誤解なきよう。
$`\quad A\ni a \overset{R}{\mapsto} b \in B`$
$`R \subseteq A\times B`$ をアンカー/リシェイプ〈anchoring, reshaping〉すると、様々なプロファイルが生じる。($`{\bf 1} = \{*\} = \{()\} = \prod( () )`$ とする。)
- $`{\bf 1} \to A\times B \In {\bf Rel}`$
または $`()\to (A, B)\In {\bf PolyRel}`$ - $`{\bf 1} \to B\times A \In {\bf Rel}`$
または $`()\to (B, A)\In {\bf PolyRel}`$ - $`A \to B \In {\bf Rel}`$
または $`(A)\to (B)\In {\bf PolyRel}`$ - $`B \to A \In {\bf Rel}`$
または $`(B)\to (A)\In {\bf PolyRel}`$ - $`B \times A \to {\bf 1} \In {\bf Rel}`$
または $`(B, A)\to ()\In {\bf PolyRel}`$ - $`A \times B \to {\bf 1} \In {\bf Rel}`$
または $`(A, B)\to ()\In {\bf PolyRel}`$
アンカー/リシェイプしても同じ名前をオーバーロードして使うと:
- $`{\bf 1}\ni * \overset{R}{\mapsto} (a, b) \in A\times B`$
- $`{\bf 1}\ni * \overset{R}{\mapsto} (b, a) \in B\times A`$
- $`A\ni a \overset{R}{\mapsto} b \in B`$
- $`B\ni b \overset{R}{\mapsto} a \in A`$
- $`B \times A \ni (b, a) \overset{R}{\mapsto} * \in {\bf 1}`$
- $`A \times B \ni (a, b) \overset{R}{\mapsto} * \in {\bf 1}`$
扱っていることは、直積集合とその部分集合だけである。だが、アンカー/リシェイプとオーバーロードに慣れるのに年単位の時間がかかってしまうことがある。
アルファ図法の基本
アルファ図法では、$`A\times B`$ の要素 $`(a, b)`$ は、座標軸上の点 $`a`$ から別な座標軸上の点 $`b`$ に向かう有向ストランド(向きが付いた紐)で表す。
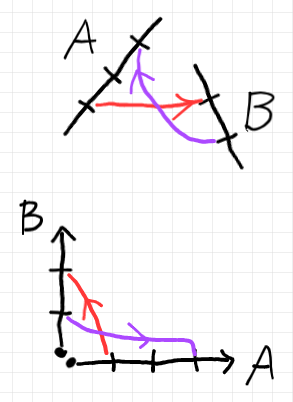
上段でも下段でも意味的差はない(同じ意味)。赤線は $`(a_1, b_2) \in A\times B`$ を、紫線は $`(b_1, a_3) \in B\times A`$ を表す。アルファさんによれば、有向ストランドは「目線移動を表す」。紫の紐なら、
- 先に座標軸 $`B`$ 上の点 $`b_1`$ を見て、目線移動して、座標軸 $`A`$ 上の点 $`a_3`$ を見たこと。
面白いのは、「同時に見る(一緒に見る)」ことも表現できること。
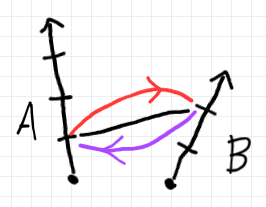
上図で:
- 赤線(有向)は、順序対 $`(a_1, b_2)`$ を表す。
- 紫線(有向)は、順序対 $`(b_2, a_1)`$ を表す。
- 黒線(無向)は、非順序対 $`[a_1, b_2] = [b_2, a_1]`$ を表す。
通常は表現が難しい非順序対〈unordered pair〉*1が、単なる無向な紐で表現できる。アルファさんは、向きが必要になるまでは向き無しで考えている。
アルファ図法によるリシェイプ
「集合 $`A`$ が2つ分、集合 $`B`$ が2つ分あります」という状況は次のように描ける。
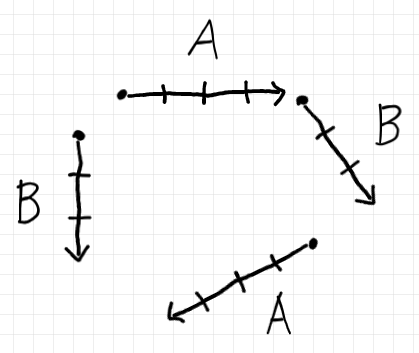
テキスト記述のためには集合に順番を付ける必要があるので、上側(12時方向)から時計回りに見て、この絵を次のリスト(テーブルスキーマ、プロファイル)で表す。
$`\quad (A, B, A, B)`$
直積を取れば以下の集合になる。
$`\quad A\times B \times A\times B`$
直積集合の要素 $`(a_2, b_2, a_1, b_1) \in A\times B \times A\times B`$ を考える。この要素は以下の黒い四角形で表現できる。
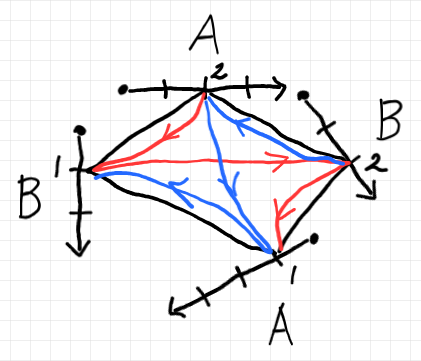
しかし、4点 $`a_2, b_2, a_1, b_1`$ を全部見ていく目線移動は一通りではない。
- 赤線は、$`(a_2, b_1, b_2, a_1) \in A\times B \times B \times A`$ を表す。
- 青線は、$`(b_2, a_2, a_1, b_1) \in B\times A \times A \times B`$ を表す。
座標軸の集まりを描き変えなくても、目線移動を変えるだけで、直積集合とその要素〈タプル〉のリシェイプ〈reshaping〉が出来るのである。
アルファ図法では、「タプルを多角形で表す」と言ったが、正確には「長さnのタプルをn点形、あるいはn点をたどる折れ線で表す」。全部の点ではなくて、一部の点だけに注目することにより射影〈projection〉も自然に考えることができる。例えば、黒い四角形の右上辺に注目すると:
$`\quad A\times B \times A\times B \ni (a_2, b_2, a_1, b_1) \mapsto (a_2, b_2)\in A\times B`$
アルファ図法によるアンカー
「部分集合としての実体は変えずにプロファイル(外部から見えるインターフェイスの仕様)だけ変える」という操作・行為を理解するのが驚くほど難しい。アルファ図法は、この操作・行為の理解の助けになる。
前節と同じ設定で、要素〈タプル〉$`(a_2, b_2, a_1, b_1) \in A\times B \times A\times B`$ を考える。この要素は部分集合 $`R\subseteq A\times B \times A\times B`$ に属するとする。
$`\quad (a_2, b_2, a_1, b_1) \in R \subseteq A\times B \times A\times B`$
部分集合 $`R`$ を、次のプロファイルで考えたとする。
$`\quad R : A\times B \to B \times A \In {\bf Rel}`$
テキストだけだと、なかなか意図が伝わらないが、次のアルファ図を併用しよう。
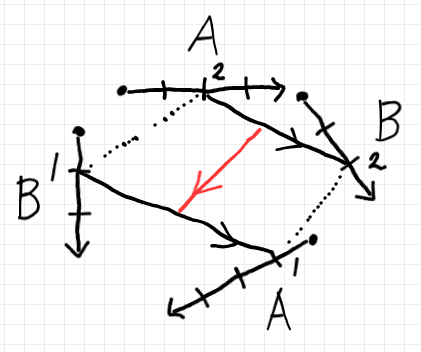
タプルを表す黒い四角形(むしろ四点形)を、右上ニ点形(有向ストランド)と、左下ニ点形に分けて、さらに「右上 → 左下」への対応(赤線)と考える。テキストで書けば:
$`\quad A\times B \ni (a_2, b_2) \overset{R}{\mapsto} (b_1, a_1) \in B\times A`$
こう書いても、やはり、テキストでは正確な情報が伝わりにくい。上記のアルファ図を参照。
同じタプル $`(a_2, b_2, a_1, b_1) \in A\times B \times A\times B`$ を、また別な解釈をすると、下図。
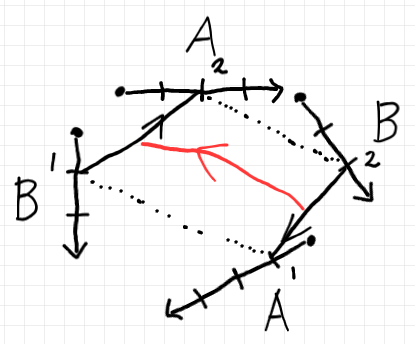
テキストで書けば:
$`\quad B\times A \ni (b_2, a_1) \overset{R}{\mapsto} (b_1, a_2) \in B\times A`$
もうひとつ別な解釈。
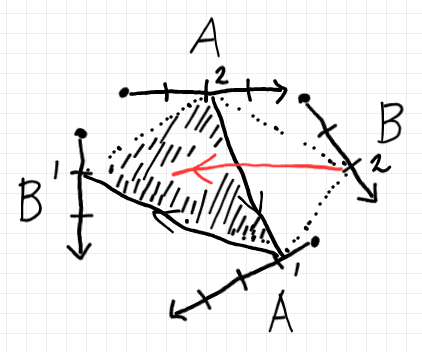
テキストで書けば:
$`\quad B \ni b_2 \overset{R}{\mapsto} (a_2, a_1, b_1) \in A\times A\times B`$
$`(a_2, a_1, b_1) \in A\times A\times B`$ は三点形あるいは三点折れ線だが、内部を斜線で塗っている。
そこに居るだけの集合/要素に対して、目線移動により関係〈非決定性写像〉だと捉え直すことをアンカー〈anchoring〉という。
中学校の関数のグラフ以来、目線移動で対応を追いかけることはやってきたはず。中学校では、直角に曲がる目線移動だったのを、アルファさんは「直角に曲がっても、直線で移動しても、カーブしても何でもいい」ことにした。それだけと言えがそれだけのこと。だが、“それだけ”のことに気づける人は少ない。
*1:定義: 直積に対する対称群の作用を考えて、商集合を作る。