モノイド閉圏の事例：計算の準備 - (2nd) 檜山正幸のキマイラ飼育記

とりあえず、記号の使い方を決めます。が、使っているうちに変更される可能性があります。決めた記法により、いくつかの定義もします。

用語のバリエーションの書き方は「用語のバリエーション記述のための正規表現」を参照。

内容：

基本的な記法
- 記号の乱用
文字の使い方の目安
グラフ射を部分に分ける
ラムダ記法
ボックス積
射のボックス積
変形
ホムグラフ
エバル〈評価射〉
カリー化〈随伴転置〉

基本的な記法

記法の決め方の方針：

誤解をしにくい。
視認性が良い。
手早く書ける。

上の項目ほど優先順位が高い。計算に使う記法では、統一性は重要ではないのでかなり不統一。

グラフAの頂点集合は A₍₀₎ とも書く。|A| = A₍₀₎ 。
グラフAの辺集合は A₍₁₎ とも書く。
s, t:A₍₁₎→A₍₀₎ は、それぞれ、辺の始点と終点。
グラフ射〈準同型写像〉f:A→B の頂点部分は f₍₀₎:A₍₀₎→B₍₀₎, 辺部分は f₍₁₎:A₍₁₎→B₍₁₎ と書く。単純グラフでは、頂点部分が決まれば、辺部分は自動的に決まる（任意性がない）。
a, a'∈|A| として、辺は a→a' と書く。単純グラフでは、両端が決まれば、辺は自動的に決まる（任意性がない）。
辺は両端で決まるので、名前を付ける必要性は少ないが、i:a→a' in A のようにも書く。i は辺の名前。単純グラフなので、i:a→a' ⇔ i = (a→a') 。
f, gがホムグラフの頂点（i.e. グラフ射）のとき、ホムグラフ（後述）の辺を α:f⇒g のようにも書く。ただし、α:f→g でもよい。「⇒」は、ホムグラフの辺であることを強調する／注記する記法。単純グラフなので、α:f⇒g ⇔ α = (f⇒g) = (f→g)
a ∈₀ A :⇔ a ∈ A₍₀₎
i ∈₁ A :⇔ i ∈ A₍₁₎

記法に慣れるために、幾つかの定義と等式を書いておく。

s(a→b) = a, t(a→b) = b
For a, b ∈₀ A, A(a, b) := {i∈A₍₁₎ | s(i) = a ∧ t(i) = b}
For f:A→B in SG
1. f₍₀₎(s(i)) = s(f₍₁₎(i))
2. f₍₀₎(t(i)) = t(f₍₁₎(i))
3. i∈A(a, b) ⇒ f₍₁₎(i)∈B(f₍₀₎(a), f₍₀₎(b)) （ここの「⇒」は「ならば」）

記号の乱用

f₍₀₎もf₍₁₎も区別せずに単にfと書くことが多い。f₍₀₎ から f₍₁₎ が決まってしまうので、乱用しても弊害は少ないと思われる。

For f:A→B in SG
1. f(s(i)) = s(f(i))
2. f(t(i)) = t(f(i))
3. i∈A(a, b) ⇒ f(i)∈B(f(a), f(b))

文字の使い方の目安

あくまで目安。守らないことも、変更することもあり得る。

文字	種別	用途・意味	備考
a, b, c, d	変数	グラフの頂点	a', b' なども
f, g, h	変数	グラフ射	SGの射、ホムグラフの頂点
i, j, k	変数	グラフの辺	あまり使わない
s, t	構成素名	辺の始点と終点
u, v, w	変数	グラフ射	主にホムグラフの頂点
x, y, z	変数	グラフの頂点	x', y' なども
A, B, C, D	変数	単純グラフ	SGの対象
F, G	変数	ホムグラフへのグラフ射	高階グラフ射
1	固有名	単頂点離散グラフ	太字のイチ
X, Y, Z	変数	単純グラフ	SGの対象
α, β, γ	変数	変形	ホムグラフの辺
γ	構成素名	内部結合	変数とかぶり
α	構成素名	結合律子	変数とかぶり
ε	構成素名	随伴の余単位	ev とも書く
η	構成素名	随伴の単位	ins とも書く
φ	構成素名	内部カリー化	ホムグラフ間の射
ψ	構成素名	内部反カリー化	ホムグラフ間の射
λ	構成素名	左単位律子
λ	メタ記号	ラムダ記号	左単位律子とかぶり
ρ	構成素名	右単位律子
σ	構成素名	対称〈スワップ〉
ι	構成素名	内部恒等
Φ	構成素名	{右}?カリー化	ホムセット間写像、通常はΛ
Ψ	構成素名	反{右}?カリー化	ホムセット間写像、通常はΓ

グラフ射を部分に分ける

f:A→B in SG を f = (f₍₀₎, f₍₁₎) と書く。Aの辺集合 A₍₁₎ が直和で A₍₁₎ = A₍₁₎₁ + A₍₁₎₂ と書けるとき、

f₍₁₎₁ := (fの、A₍₁₎₁ への制限)
f₍₁₎₂ := (fの、A₍₁₎₂ への制限)

として、次の書き方をする。

f = (f₍₀₎, f₍₁₎₁ | f₍₁₎₂)

この書き方では、「,」より「|」のほうが優先度（結合の強度）が高い。

「,」、「|」では視認性が悪いときは、ALSO, OR を使う。

f = (f₍₀₎ ALSO f₍₁₎₁ OR f₍₁₎₂)

ラムダ記法

通常のインフォーマルな型付きラムダ記法を用いるが、'λ'の肩に 0, 1 を付けることがある。

λ⁰x∈X.( ... ) は、λx∈₀X.( ... ) 、あるいは、λx∈X₍₀₎.( ... ) と同じ。グラフ射の頂点部分を表す。
λ¹x∈X.( ... ) は、λx∈₁X.( ... ) 、あるいは、λx∈X₍₁₎.( ... ) と同じ。グラフ射の辺部分を表す。
式の値の型は、「∈ B」のような書き方で示すが、このとき「∈₁B」や「∈B₍₁₎」とは書かない。頂点・辺の区別（要素の次元）は文脈から読み取る。
前節の区切りキーワード ALSO, OR を使って組み合わせる。

同語反復だが、

f:A→B = (
  λ⁰a∈A.(f₍₀₎(a) ∈B)
  ALSO
  λ¹a→a'∈A.(f₍₁₎(a→a') ∈B)
)

または、

f:A→B = (
  λ⁰a∈A.(f₍₀₎(a) ∈B)
  ALSO
  λ¹a→a'∈A.(f₍₀₎(a)→f₍₀₎(a') ∈B)
)

f:A→B, g:C→D に対する f×g の定義：

f×g:A×C→B×D := (
  λ⁰(a, c)∈A×C.( (f(a), g(c)) ∈B×D )
  ALSO
  λ¹(a, c)→(a', c')∈A×C.( (f(a→a'), g(c→c')) ∈B×D )
)

ボックス積

(A□B)₍₀₎ := A₍₀₎×B₍₀₎
(A□B)₍₁₎ := A₍₁₎×B₍₀₎ + A₍₀₎×B₍₁₎

s, t の定義は（通常のラムダ記法で示す）：

s:(A□B)₍₁₎→(A□B)₍₀₎ := (
  λ(a→a', b)∈A₍₁₎×B₍₀₎.( (a, b) ∈A₍₀₎×B₍₀₎ )
  OR
  λ(a, b→b')∈A₍₀₎×B₍₁₎.( (a, b) ∈A₍₀₎×B₍₀₎ )
)

t:(A□B)₍₁₎→(A□B)₍₀₎ := (
  λ(a→a', b)∈A₍₁₎×B₍₀₎.( (a', b) ∈A₍₀₎×B₍₀₎ )
  OR
  λ(a, b→b')∈A₍₀₎×B₍₁₎.( (a, b') ∈A₍₀₎×B₍₀₎ )
)

1 に関して、1₍₀₎ = {0}, 1₍₁₎ = {} = 空集合。1□B を計算してみる。

(1□B)₍₀₎ := 1₍₀₎×B₍₀₎ $\cong$ B₍₀₎
(1□B)₍₁₎ := 1₍₁₎×B₍₀₎ + 1₍₀₎×B₍₁₎ = 1₍₀₎×B₍₁₎ $\cong$ B₍₁₎

s, t の定義は（通常のラムダ記法で示す）：

s:(1□B)₍₁₎→(1□B)₍₀₎ := (
  λ(a, b→b')∈1₍₀₎×B₍₁₎.( (0, b) ∈1₍₀₎×B₍₀₎ )
)
 λb→b'∈B₍₁₎.(  b ∈B₍₀₎ )

t:(1□B)₍₁₎→(1□B)₍₀₎ := (
  λ(a, b→b')∈1₍₀₎×B₍₁₎.( (0, b') ∈1₍₀₎×B₍₀₎ )
)
 λb→b'∈B₍₁₎.(  b' ∈B₍₀₎ )

以上で、1□B $\cong$ B が示せた。より直接的な λ_B:1□B→B in SG の表示は（'λ'がかぶっていて、困ったことだが）：

λ_B:1□B→B := (
  λ⁰(0, b)∈1□B.( b ∈B) /* 頂点部分 */
  ALSO
  λ¹(0, b→b')∈1□B.( b→b' ∈B)  /* 辺部分 */
)

この定義に対して、次が可換になるので、λ_B はグラフ射。

$\require{AMScd} \begin{CD} ({\bf 1}\Box B)_{(1)} @>{(\lambda_B)_{(1)}}>> B_{(1)} \\ @V{s, t}VV @VV{s, t}V \\ ({\bf 1}\Box B)_{(0)} @>{(\lambda_B)_{(0)}}>> B_{(0)} \end{CD}$

射のボックス積

f:A→B, g:C→D in SG に対して、f□g を定義する。

f□g:A□C→B□D := (
 λ⁰(a, c)∈A□C.( (f(a), g(c)) ∈B□D) /* 頂点部分 */
 ALSO
 λ¹(a→a', c)∈A□C.( (f(a→a'), g(c)) ∈B□D) /* 辺部分 その1 */
 OR
 λ¹(a, c→c')∈A□C.( (f(a), g(c→c')) ∈B□D) /* 辺部分 その2 */
)

実際には、次の可換図式が必要になる。

$\begin{CD} (A\Box C)_{(1)} @>(f \Box g)_{(1)}>> (B\Box D)_{(1)} \\ @V{s, t}VV @VV{s, t}V \\ (A\Box C)_{(0)} @>(f \Box g)_{(0)}>> (B\Box D)_{(0)} \end{CD}$

変形

A, B∈|SG| として、A₍₀₎ から B₍₁₎ の写像を変形〈deformation〉と呼ぶことにする（一般的な用語ではない）。変形を次の形のラムダ記法で書く。

λ⁰¹a∈A.( ... ∈B)

「...」の部分には、Bの辺を表す式が入る。Aが反射的なとき、頂点にその自己ループ辺を対応させる変形は：

λ⁰¹a∈A.( a→a ∈A)

αが A₍₀₎→B₍₁₎ の形の変形であることを α:A (0→1) B と書く。ぎごちない記法だが、どうせたいして使わないからいいとする。

α:A (0→1) B に対して、写像 α;s, α;t :A₍₀₎→B₍₀₎ が決まる。α;s, α;t は、単なる頂点集合間の写像なので、それがグラフ射を定義するとは限らない。が、もし次の条件が成立しているなら、αをfからgへの変形と呼ぶ。

α;s = f :A→B かつ α;t = g :A→B

このとき、α:f⇒g と書く。AとBの情報を添えたいときは、α:f⇒g: A (0→1) B と書く（が、面倒だからほとんど書かない）。今後、考える変形は、両端がグラフ射になっているようなものである。

[補足]両端がグラフ射にならない変形の例：

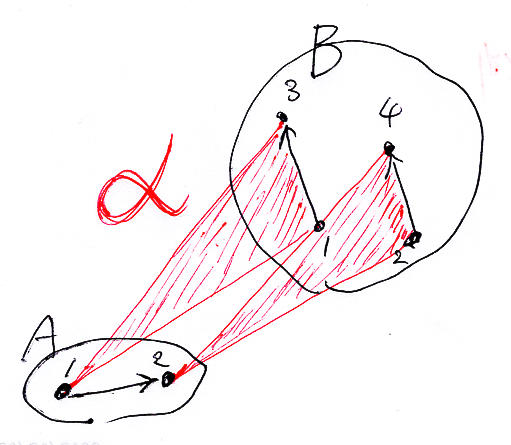
グラフ A ： A₍₀₎ = {1, 2}, A₍₁₎ = {1→2}
グラフ B ： B₍₀₎ = {1, 2, 3, 4}, B₍₁₎ = {1→3, 2→4}
変形 α ： α(1) = 1→3, α(2) = 2→4

変形αの両端を f, g とすると：

ソース側： f(1) = 1, f(2) = 2
ターゲット側： g(1) = 3, g(2) = 4

fもgもグラフ射にはなってない。Aの辺 1→2 の送り先が存在しない。
[/補足]

ホムグラフ

圏はSGしか考えないので、次の略記をする。

Hom(A, B) = Hom_SG(A, B) = SG(A, B)

2つの単純グラフ A, B に対して、そのホムグラフ hom(A, B) を次のように定義する。

|hom(A, B)| = hom(A, B)₍₀₎ := Hom(A, B)
For f, g∈|hom(A, B)|,
hom(A, B)(f, g) := {α | α:f⇒g という変形}

この定義から、ただちに hom(A, B) が単純グラフだと言えるわけではないが、容易に次は分かる。

A, B∈|SG| ⇒ hom(A, B)∈|SG|

つまり、

hom(A, B)(f, g) は空集合か単元集合

hom(A, B) は正確に言えば内部ホムグラフで、Hom(A, B) とは次の点で違う。

Hom(A, B) は外部ホムセット＝普通のホムセットで、単なる集合、グラフ構造は持たない。SGの対象とも考えない。
hom(A, B) は内部ホム対象で、グラフ構造を持ち、SGの対象と考える。

エバル〈評価射〉

A, B∈|SG| に対して、ev_A,B:hom(A, B)□A→B を次のように定義する。

ev_A,B:hom(A, B)□A→B := (
 λ⁰(f, a)∈hom(A, B)□A.( f(a) ∈B)
 ALSO
 λ¹(f⇒f', a)∈hom(A, B)□A.( f(a)→f'(a) ∈B)
 OR
 λ¹(f, a→a')∈hom(A, B)□A.( f(a→a') ∈B)
)

ev_A,Bは、上記のラムダ記法で定義されるSGの射である。実際には、次の可換図式が必要になる。

$\begin{CD} (hom(A, B)\Box A)_{(1)} @>{(ev_{A,B})_{(1)}}>> B_{(1)} \\ @V{s, t}VV @VV{s, t}V \\ (hom(A, B)\Box A)_{(0)} @>{(ev_{A,B})_{(0)}}>> B_{(0)} \end{CD}$

カリー化〈随伴転置〉

カリー化〈随伴転置〉は、ホムセット（外部ホムセット）のあいだの写像であり、グラフ射ではない。Hom(A□B, C) の要素 f に対して、A から hom(B, C) へのグラフ射を対応させる。値であるグラフ射の頂点部分は「頂点→グラフ射」で、辺部分は「辺→変形」となる。

Φ_A,B,C:Hom(A□B, C)→Hom(A, hom(B, C)) :=
  λf∈Hom(A□B, C).(
     λ⁰a∈A.(
        (λ⁰b∈B.( f(a, b) ∈C)
         ALSO
         λ¹b→b'∈B.( f(a, b→b') ∈C)
        ) ∈hom(B, C)
     )
     ALSO
     λ¹a→a'∈A.(
       (λ⁰¹b∈B.( f(a→a', b) ∈C)) ∈hom(B, C)
     )
  )

コメント付き：

Φ_A,B,C:Hom(A□B, C)→Hom(A, hom(B, C)) :=
  λf∈Hom(A□B, C).( /* グラフ射 f:A□B→C が与えられる */

     /* ここから下に、
        f に対する値である高階グラフ射 F:A→hom(B, C)
        を記述する
     */

     /* 高階グラフ射 F の頂点部分 */
     λ⁰a∈A.(
        /* a∈A₍₀₎ に対して、
           F(a) はグラフ射 F(a):B→C
        */
        (λ⁰b∈B.( f(a, b) ∈C) /* F(a)(b) := f(a, b) */
         ALSO
         λ¹b→b'∈B.( f(a, b→b') ∈C) /* F(a)(b→b') := f(a, b→b') */
        ) ∈hom(B, C) /* end of グラフ射 F(a) */
     ) : A→hom(B, C) /* end of F の頂点部分 */
     ALSO
     /* 高階グラフ射 F の辺部分 */
     λ¹a→a'∈A.( /* 辺 a→a' が与えられる */
       /* F(a→a') は変形 F(a→a'):B (0→1) C */
        ( /* 変形は、Bの頂点 b にCの辺を対応させる */
         λ⁰¹b∈B.(
           f(a→a', b) ∈C)
        ) ∈hom(B, C) /* end of 変形 F(a→a') */
     ) : A→hom(B, C)  /* end of F の辺部分 */
  )