限量子付き論理式の解釈 (G2 A5)

RSS-G2

※この記事は「記事5」

この記事は、第一期セミナーで受けた質問に対して書かれた過去記事を元にリライトしたものです。一般的な内容は別記事「論理式の集合とは何か？」に書いてあり、セミナー受講を前提にした内容は本記事で書きます。限量子の意味と使い方がイマイチ不安だ、という方は目を通してみてください。

内容：

論理式の意味とは

事前の予備知識は：

形式化された（データ化された）命題、つまり論理式〈formula〉Pに対して、その意味とは、スコットブラケット（の値）〚P〛のことです。国語辞書や世間の常識などは一切マッタクひたすら何の関係もなく、素朴集合論のなかで〚P〛を定義することが意味を与えることです。

このとき、コンテキストがないと〚P〛は定義できません。しかし、コンテキストは省略する習慣（悪習）があり、コンテキストの書き方の合意さえありません*1。ここでは、コンテキストと論理式をカンマ、または縦棒で区切ることにします。例は：

  • (x, y, z∈R, n∈Z), n×x ≧ y
  • (x, y, z∈R, n∈Z)| n×x ≧ y

縦棒を使う場合は、コンテキストを囲む丸括弧は省略してもいいとします（付けてもいいけど）。

  • x, y, z∈R, n∈Z| n×x ≧ y

スコットブラケットの値は、コンテキストのドメインの部分集合になります。例では、Dom(x, y, z∈R, n∈Z) = R3×Z がコンテキストのドメインなので、

  • 〚x, y, z∈R, n∈Z| n×x ≧ y〛 ⊆ R3×Z

または、同じことですが、Powをベキ集合だとして、

  • 〚x, y, z∈R, n∈Z| n×x ≧ y〛 ∈ Pow(R3×Z)

コンテキストなしではスコットブラケットを定義できないので、論理式Pに対して〚P〛と書いてあったら、Pにコンテキストが含まれているか、またはコンテキストを省略していると考えます。

限量子による束縛

「限量子が分かってない」という方は、まず次を読んでください。

限量子による束縛は、論理式に含まれる変数、コンテキストに含まれる変数を考慮する必要があります。

  1. 限量子の束縛変数は、論理式に現れなくてもよい。空虚な束縛〈vacuous quantification〉も許す。それどころか、空虚な束縛は極めて重要である。興味があれば、「空虚な束縛とEPペア」参照。
  2. 限量子の束縛変数は、コンテキストに現れなくてはならない。

例えば、コンテキストが (x, y, z∈R, n∈Z) ならば、全称限量子'∀'に関して次の束縛はどれも有効です（真偽は問題にしてません）。

  1. ∀x∈R.( n×x ≧ y )
  2. ∀y∈R.( n×x ≧ y )
  3. ∀z∈R.( n×x ≧ y )
  4. ∀n∈Z.( n×x ≧ y )

しかし、次の束縛は許されません。コンテキスト (x, y, z∈R, n∈Z) に、変数 s, k は入ってないからです。

  1. ∀s∈R.( n×x ≧ y )
  2. ∀k∈Z.( n×x ≧ y )

束縛は、論理式だけに対する操作ではなくて、束縛によりコンテキストも変化します。コンテキストの変化がとても重要です。

  • (x, y, z∈R, n∈Z), n×x ≧ y ← 束縛前
  • (y, z∈R, n∈Z), ∀x∈R.( n×x ≧ y) ← xによる束縛
  • (y, z∈R), ∃n∈Z.∀x∈R.( n×x ≧ y) ← x, n による束縛
  • (y∈R), ∃z∈R.∃n∈Z.∀x∈R.( n×x ≧ y) ← x, n, z による束縛

変数とその型（変域の集合）が、コンテキストから限量子へと移動するのです。コンテキストの変数を使い切るとそれ以上の束縛は出来なくなります。

  • (), ∀y∈R.∃z∈R.∃n∈Z.∀x∈R.( n×x ≧ y) ← x, n, z, y による束縛

コンテキストを増やす操作〈thinning | weakening〉はいつでもやって構いませんが、それは明示的に行うべきものです。

コンテキストを省略して、コンテキストへの操作も暗黙的にやってしまうことが、議論を不透明・曖昧にしてしまいます。事情が理解できるまでは、省略や暗黙の操作はやめましょう。

同時に2個以上の変数を束縛することも許します。例えば：

  • (z∈R, n∈Z), ∀x, y∈R.( n×x ≧ y) ← x, y で同時に束縛
  • (), ∃z∈R, n∈Z.∀x, y∈R.( n×x ≧ y) ← x, yで同時に束縛、z, n で同時に束縛

存在限量子の意味

AとBは集合だとして、x, y は（形式化された）変数とします*2。コンテキスト (x∈A, y∈B) があるとして、xを存在限量子'∃'で束縛することを考えます。

  • 束縛の前： (x∈A, y∈B), P
  • 束縛の後： (y∈B), ∃x∈A.P

束縛前の意味（＝スコットブラケットの値）が分かっているとして、束縛後の意味を定義します。余計なことは考えないで、淡々とスコットブラケットの計算法を示します。

束縛前のスコットブラケットは、

  • 〚x∈A, y∈B| P〛 ⊆ A×B

これは既知として、次の値を定義します。

  • 〚y∈B| ∀x∈A.P〛 ⊆ B

実際の定義は次のとおり：

  • 〚y∈B| ∀x∈A.P〛 := π2*(〚x∈A, y∈B| P〛)

ここで出てきた π2* を次節で説明します。

像集合と射影写像

一般に（完全に一般論）、X, Y が集合で、f:X→Y が写像のとき、S⊆X に対して、

  • f*(S) := {y∈Y | f(x) = y かつ y∈S であるxが存在する}

f*(S) を、fによるSの像集合〈image set〉または単に像〈image〉と呼びます。f*自体は、f*:Pow(X)→Pow(Y) という写像です。fとf*は、しばしば区別しないでfと書かれますが、別な写像です。

像集合の定義で、「かつ」と「存在する」が出てきてます。これらは、メタ数学（通常の数学）のメタ論理（形式化されてない、数理論理以前の普通の素朴な古典論理）のメタ論理記号（日本語だけど）です。

形式化された'∃'の意味の定義に、メタ論理の「存在する」を使うのは循環論法ではないか？ -- そんなことはありません。メタ論理の「存在する」は数学する誰もが日々使っているもので、それを使う行為は普通のことです。普通にやっていることをイチイチ疑ったり文句を言い出すと何も出来なくなります。

次に、射影と呼ばれる写像 π1, π2 を定義します。

  • π1:A×B→A, π1(a, b) := a これが第一射影〈first projection〉
  • π2:A×B→B, π2(a, b) := b これが第ニ射影〈second projection〉

ほんとは、π1((a, b))（内側はペアを囲む括弧、外側は引数を囲む括弧）と書くべきですが、面倒なので括弧を省略してます。また、π1, π2 と下付き添字がよく使われますが、ここでは添字ではなくて番号を関数名の一部にしています。

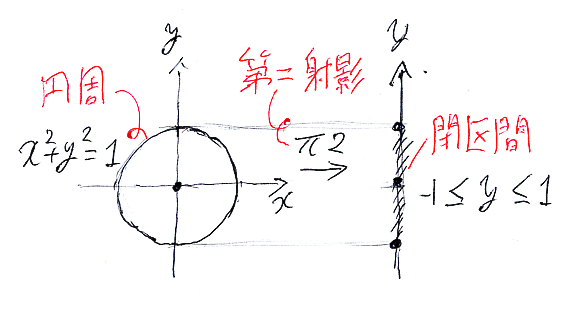
前節の π2*(〚x∈A, y∈B| P〛) は、第ニ射影の像集合のことです。例えば、〚x∈R, y∈R| x2 + y2 = 1〛 は図形として単位円周です。〚y∈R| ∃x∈R.( x2 + y2 = 1 )〛 = π1*(〚x∈R, y∈R| x2 + y2 = 1〛) は、単位円周をy方向に射影した像集合なので、-1から1の閉区間 {y∈R | -1 ≦ y ≦ 1} となります。

一般に、〚x∈A, y∈B| P〛 = V ⊆ A×B のとき、

  • 〚y∈B| ∃x∈A.P〛 = π2*(V) ⊆ B

全称限量子の意味と練習

存在限量子と全称限量子のあいだには次の関係があります。

  • ∀x∈A.P ⇔ ￢∃x∈A.￢P

同値な論理式のスコットブラケット（の値）は等しい（これは証明できるメタ定理）ので、

  • 〚∀x∈A.P〛 = 〚￢∃x∈A.￢P〛

コンテキストも考慮すれば：

  • 〚y∈B| ∀x∈A.P〛 = 〚y∈B| ￢∃x∈A.￢P〛

したがって、全称限量子を持つ論理式のスコットブラケットは次のように計算できます。（右肩の'c'は補集合）

  • 〚y∈B| ∀x∈A.P〛 = 〚y∈B| ￢∃x∈A.￢P〛 = (π2*(〚x∈A, y∈B| P〛c))c

これはあまり分かりやすくありません。もう少しストレートな解釈もありますが、それは、練習をやっていくなかで見出してみてください。

練習問題：

*1:僕自身もこれといって決めてなくて、その場その場でテキトーに書いてますが、これは良くないですね。それと、コンテキストと限量子の束縛部分の構文も統一すべきです。今後は気を付けます。

*2:ここでの文字'x', 'y'は変数を表す変数名です。