射影＝写像となる文脈 - (2nd) 檜山正幸のキマイラ飼育記

$\newcommand{\In}{\text{ in } } \newcommand{\id}{\mathrm{id} } %\newcommand{\dom}{\mathrm{dom} } %\newcommand{\cod}{\mathrm{cod} } \newcommand{\cat}[1]{\mathcal{#1} } \newcommand{\mrm}[1]{\mathrm{#1} } %\newcommand{\twoto}{\Rightarrow} %\newcommand{\imp}{\mathop{=\!\!\triangleright} } \newcommand{\Imp}{\Rightarrow } % \require{color}% \newcommand{\Keyword}[1]{ \textcolor{green}{ \bf \text{#1} } }% \newcommand{\For}{\Keyword{For }} %\newcommand{\Macro}{\Keyword{Macro }} \newcommand{\Let}{\Keyword{Let }}% 一箇所使っていた %\newcommand{\WeWillDefine}{\Keyword{WeWillDefine }}% %\newcommand{\WeDefine}{\Keyword{WeDefine }}% \newcommand{\Where}{\Keyword{Where }}% \newcommand{\Justification}{\Keyword{Justification }}% %\newcommand{\Using}{\quad\Keyword{Using }} %\newcommand{\ChangeNotation}{\quad\Keyword{ChangeNotation }} %\newcommand{\Substitution}{\quad\Keyword{Substitution }} %\newcommand{\When}{\Keyword{When } } \newcommand{\WeAssert}{\Keyword{WeAssert }} \newcommand{\WeIntroduce}{\Keyword{WeIntroduce }} %\newcommand{\WeInstantiate}{\Keyword{WeInstantiate }} \newcommand{\WeConstruct}{\Keyword{WeConstruct }} \newcommand{\From}{\Keyword{ From } } %\newcommand{\WeAddmit}{\Keyword{WeAddmit }} \newcommand{\Requires}{\Keyword{Requires }} \newcommand{\As}{\Keyword{ As } } \newcommand{\IsA}{\Keyword{ IsA } } \newcommand{\Of}{\Keyword{ Of } } \newcommand{\ClassOf}{\Keyword{ClassOf } } \newcommand{\Things}{\Keyword{ Things} } \newcommand{\Assuming}{\Keyword{Assuming } } \newcommand{\Alias}{\Keyword{Alias } } %\newcommand{\To}{\Keyword{ To } } \newcommand{\Begin}{\Keyword{Begin} } \newcommand{\End}{\Keyword{End} }$ ある文脈では、「射影」は直積の射影ではなく全射でさえない写像を意味する。つまり、「射影」と「写像」は同義語。こういう“文脈”をどうしたら（ある程度）形式化できるだろうか？

内容：

記述方法
ファミリー
バンドル
- バンドル：
- 全射バンドル：
名前構造
さらに同義語
Graphvizソース

記述方法

well-traind people のあいだならコミュニケーション可能だと信じている。

半形式的記述を用いる。
$\Begin$ と $\End$ はブロック（ひとかたまりの記述）の区切りが分かりにくいときに使う。ハッキリと区切れるときは使う必要はない。
ブロックは名前空間を持ち、ブロック内で宣言された名前はブロック・ローカルになる。
ブロック自体の名前はカレント（今の話題）のグローバル名前空間に入る。
「今の話題」は、プログラミング言語でいうモジュールやパッケージになるだろう。

ファミリー

ファミリー：

$\WeIntroduce (A, F) \As \text{family} \\ \Where\\ \quad A \in |{\bf Set}| \As \text{index\{ing\}? set}\\ \quad F: A \to |{\bf Set}| \In {\bf SET} \As \text{family map}\\ \End\\ \Alias \text{\{indexed | parametesized\} family of sets} := \text{family}$

名前 indexing set の修飾付き名〈qualified name〉は以下のようになる（どれも使える）。階層の区切りはスラッシュを使う（ドットは他の目的で使いそうだから）。

$\text{family/}A$
$\text{family/indexing set}$
$\text{family/index set}$
$\text{indexed family of sets/}A$
$\text{indexed family of sets/indexing set}$
$\text{indexed family of sets/index set}$
その他は省略

もちろん日本語でもよい。スラッシュの代わりに太字の「の」を使ってみる。

族の $A$
族のインデックス集合〈indexing set〉
族のインデックス集合〈index set〉
インデックス付き集合族の $A$
インデックス付き集合族のインデックス集合〈indexing set〉
インデックス付き集合族のインデックス集合〈index set〉
その他は省略

無共分ファミリー：

$\Assuming (A, F) \IsA \text{family} \\ \WeIntroduce (A, F) \As \text{disjoint family} \\ \Requires\\ \quad \forall a, b\in A.\, a \ne b \Imp F(a)\cap F(b) = \emptyset \As \text{disjointness}$

ファミリー → 無共分ファミリー:

$\WeConstruct \text{disjoin family }(A, G) \From \text{family }(A, F)\\ \As \text{make-disjoint-family | 族の無共分化}\\ \Where\\ \quad A := A\\ \quad G := \lambda\, x\in A. \{x\}\times F(x)\\ \Justification\\ \quad \forall a, b\in A.\, a \ne b \Imp G(a)\cap G(b) = \emptyset$

写像（冗長な定義）：

$\WeIntroduce (X, Y, f) \As \text{map}\\ \Where\\ \quad X \in |{\bf Set}| \As \text{domain}\\ \quad Y \in |{\bf Set}| \As \text{codomain}\\ \quad f :X \to Y \In {\bf Set} \As \text{itself}$

写像 → 無共分ファミリー：

$\WeConstruct \text{disjoint family } (A, F) \From \text{map }(X, A, f)\\ \As \text{make-family-of-map}\\ \Where\\ \quad A := A \As \text{indexing set}\\ \quad F := \lambda\, a\in A.\{x\in X \mid f(x) = a \} \As \text{family map}\\ \Justification \\ \quad \forall a, b\in A.\, a \ne b \Imp F(a)\cap F(b) = \emptyset$

無共分ファミリー → 写像：

$\WeConstruct \text{map }(X, A, f) \From \text{disjoint family } (A, F)\\ \As \text{make-map-of-disjoint-family}\\ \Where\\ \quad X := \bigcup_{a\in A}F(a) \As \text{domain}\\ \quad A := A \As \text{codomain}\\ \quad f := \lambda\, x\in X.\varepsilon!\,a\in A. x\in F(a) \As \text{itself}\\ \Justification \\ \quad \forall x\in X. \exists!\,a\in A. x\in F(a)$

無共分ファミリーと写像の同型：

$\text{make-family-of-map} :\\ (\ClassOf \text{map}\Things) \to (\ClassOf \text{disjoint family}\Things) \In {\bf SET}\\ \text{make-map-of-disjoint-family} : \\ (\ClassOf \text{disjoint family}\Things) \to (\ClassOf \text{map} \Things) \In {\bf SET}\\ \WeAssert\\ \quad \text{make-map-of-disjoint-family} ; \text{make-family-of-map} = \\ \quad \id_{(\ClassOf \text{disjoint family}\Things)} \In {\bf SET}\\ \quad \text{make-family-of-map} ; \text{make-map-of-disjoint-family} = \\ \quad \id_{(\ClassOf \text{map}\Things)} \In {\bf SET}$

自然言語で一言でいえば：

無共分ファミリーという概念と写像という概念は、事実上同じである。

バンドル

バンドル：

$\Begin\\ \Assuming (A, F) \IsA \text{disjoint family}\\ \Assuming (X, A, f) \IsA \text{map}\\ \WeIntroduce (X, A, f, F) \As \text{bundle}\\ \Requires\\ \quad \text{map }(X, A, f) = \text{make-map-of-disjoint-family}(\text{disjoint family }(A, F))\\ \Alias \text{base set} := A\\ \Alias \text{total set} := X\\ \Alias \text{projection} := f\\ \Alias \text{fibre of } := F\\ \End\\ \Alias \text{fibration} := \text{bundle}$

バンドルという概念は、make-map-of-disjoint-family, make-family-of-map で結ばれた族と写像の両方を一度に考えている。

写像からバンドルを一意に構成でき、ファミリーからもバンドルを一意に構成できる。つまり、

写像、無共分ファミリー、バンドルという3つの概念は、事実上同じである。
任意のファミリーは無共分化できるので、写像、任意のファミリー、バンドルという3つの概念も、ほぼ同じである。

全射バンドル：

$\Assuming (X, A, f, F) \IsA \text{bundle}\\ \WeIntroduce (X, A, f, F) \As \text{surjective bundle}\\ \Requires\\ \quad \forall a\in A.\, F(a) \ne \emptyset \As \text{sujective condition}$

次のように書ける。

$\Let B := \text{bundle} (X, A, f, F)\\ \WeAssert\\ \quad X = (\text{total set} \Of B)\\ \quad A = (\text{base set} \Of B)\\ \quad f = (\text{projection} \Of B)\\ \quad F = (\text{family map} \Of B) = (\text{fiber of} \Of B)$

全射バンドルの言い換え：

$\Assuming B \IsA \text{bundle}\\ \WeIntroduce B \As \text{surjective bundle}\\ \Requires\\ \quad \forall a\in (\text{base set} \Of B).\, \text{'fibre of'}(a) \ne \emptyset$

日本語に翻訳すると：

$B$ はバンドルだとして、
$B$ が全射バンドルであるとは、
$B$ のベース集合の任意の要素に対してその要素のファイバーが空ではないこと。

次は明らかだろう。

全射写像、値が空集合にならない無共分ファミリー、全射バンドルという3つの概念は、事実上同じである。

名前構造

グローバル名前空間にグローバル・ルートノードがあり、ルートから名指し〈naming | designation by name〉の有向辺をたどって各種概念の名前に到達できる。

グローバルルートは星印
構造（の概念）は二重丸
構造の名指しは破線矢印
名前は必ず有向辺（名指しの辺）に付く。ノードには付かない！

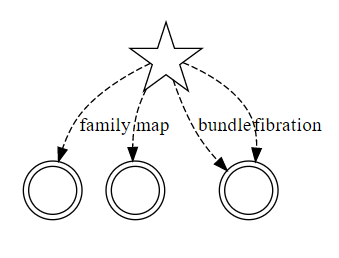
略記として、名前のひとつをノードに付けてもいい。が、あくまで略記。名前は必ず有向辺（名指しの辺）に付く。
別名は自己ループ辺として書いたよい。が、実際はグローバルルートからの有向辺（名指しの辺）に別名が付く。

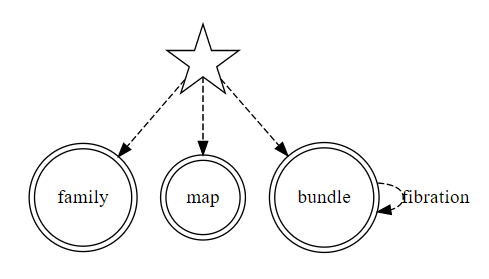
グローバルルートからの有向辺（名指しの辺）を省略してよい。
あくまで省略。略記で構造を誤解しないように。

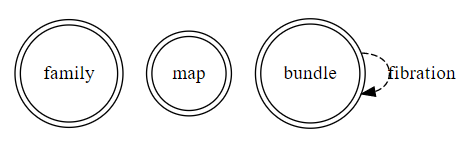
バンドルの名前構造は次のようになる。詳細は図の後に。

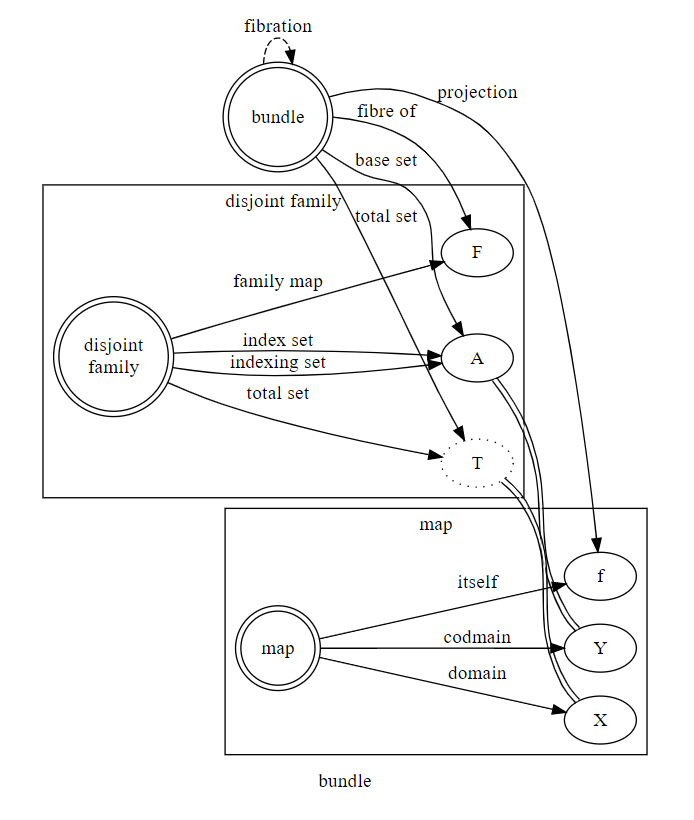
構造のノード（二重丸）は名前空間を持つ。
構造の名前空間には、その構造自体を表すローカルルートがある。
ローカルルートから出る名指しの辺（実線矢印）には、構成素名〈役割名〉が乗る。
構成素は楕円ノード。
バンドルの名前空間内に、無共分ファミリーの名前空間と写像の名前空間（のコピー達）が包含〈containment〉される。
写像の余域とファミリーのインデックス集合は同一なので、二重線（イコール）で結ばれる。張り合わさって重なると思ってよい。
点線のノード「トータル集合」はもとの無共分ファミリーの名前空間にはないが、追加した。
写像の域とファミリーのトータル集合は同一なので、二重線（イコール）で結ばれる。
「射影」や「底集合」は、バンドルという構造の構成素名である。
バンドルの構成素名「射影」は、写像の構成素名「それ自身」と同じ概念をさす。
これが、「ある文脈では、「射影」と「写像」が同義語となる」メカニズム。

さらに同義語

$\Alias \text{container} := \text{bundle}\\ \Alias \text{container schema} := \text{bundle}\\ \Alias \text{corolla forest} := \text{bundle}\\ \Alias \text{forest of corollas} := \text{bundle}\\ \Alias \text{arena} := \text{bundle}\\ \Alias \text{dependent set} := \text{bundle}\\ \Alias \text{sigma type} := \text{bundle}\\ \Alias \text{dependent sum type} := \text{bundle}\\ \Alias \text{dependent product type} := \text{bundle}\\$

Graphvizソース

/* global naming official */
digraph {
  global[shape=star, label=""]

  family[shape="doublecircle", label=""]
  map[shape="doublecircle", label=""]
  bundle[shape="doublecircle", label=""]

  global -> family[style=dashed,label="family"]
  global -> map[style=dashed,label="map"]
  global -> bundle[style=dashed,label="bundle"]
  global -> bundle[style=dashed,label="fibration"]
}

/* global naming shorthand */
digraph {
  global[shape=star, label=""]

  family[shape="doublecircle"]
  map[shape="doublecircle"]
  bundle[shape="doublecircle"]

  global -> family[style=dashed]
  global -> map[style=dashed]
  global -> bundle[style=dashed]
  bundle -> bundle[style=dashed, label="fibration"]
}

/* global naming abbrev */
digraph {

  family[shape="doublecircle"]
  map[shape="doublecircle"]
  bundle[shape="doublecircle"]
  
  bundle -> bundle[style=dashed, label="fibration"]
}

```graphviz
/* name structure of bundle */
digraph {
 rankdir = LR
 label="bundle"

 bundle[shape=doublecircle]
 bundle -> bundle[label="fibration", style=dashed]
 subgraph cluster_fam {
   label="disjoint family"
   family[shape=doublecircle, label="disjoint\n family"]
   famMap[label="F"]
   ind[label="A"]
   tot[label="T", style=dotted]
   family -> ind[label="indexing set"]
   family -> ind[label="index set"]
   family -> famMap[label="family map"]
   family -> tot[label="total set"]
 }
 subgraph cluster_map {
   label="map"
   map[shape=doublecircle]
   dom[label="X"]
   cod[label="Y"]
   it[label="f"]
   map -> dom[label="domain"]
   map -> cod[label="codmain"]
   map -> it[label="itself"]
 }
 ind -> cod[color="black:white:black";arrowhead=non]
 tot -> dom[color="black:white:black";arrowhead=non]

 bundle -> it[label="projection"]
 bundle -> ind[label="base set"]
 bundle -> tot[label="total set"]
 bundle -> famMap[label="fibre of"]

}