ネコひねり問題のセッティング（だけ） - (2nd) 檜山正幸のキマイラ飼育記

Mさんの話からの類推。既存の資料を調べたりはしてない。セッティングだけで、どう解くかは分からない。[追記 date="翌日"]Mさんに資料をいただきました。色々と違っていた。後で別記事にするかも。[/追記] $\newcommand{\R}{ {\bf R} }$

2つの主バンドルを定義する。

$\pi : \R^3 \times (ONFrame(3)\times ONFrame(3)) \to \R^3$
自明バンドル、構造群は $SO(3)\times SO(3)$
$\pi : ONFrame(3)\times ONFrame(3) \to S^2 \times S^2$
構造群は $SO(2)\times SO(2)$

内容：

ネコのモデル
正規直交フレームと姿勢空間
位置空間と主バンドル
ネコの運動
もうひとつの主バンドル
問題における制約

ネコのモデル

伝統的に2つの円筒でモデル化するようだが、ジョイントされた2つの剛体なら何でもいいので（[追記]なんでもよくはない[/追記]）、2つのL字形のロッドを使う。片方を（ネコの）上半身（下図の青）、もう一方を下半身（下図の赤）と呼ぶ。中心点からの上半身の線に直行する線をハナスジ（鼻筋）、下半身の線に直行する線をシッポ（尻尾）と呼ぶ。

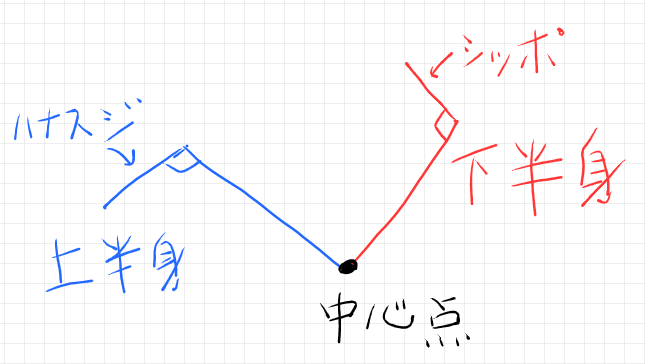
本物の猫では、顔も尻尾も激しく動かすだろうが、このモデルではハナスジ／シッポが胴体に固定されていて動かないとする。

中心点（ジョイントの所）の位置をネコの位置と約束する。

正規直交フレームと姿勢空間

3次元空間の正規直交フレーム $e = (e_1, e_2, e_3)$ と $f = (f_1, f_2, f_3)$ を次のように決める。

名前	説明
e₁	中心点から出る上半身の矢線
e₂	ハナスジの矢線
e₃	e₁, e₂ に右手系で直交
f₁	中心点から出る下半身の矢線
f₂	シッポの矢線
f₃	f₁, f₂ に右手系で直交

$\R^3$ の正規直交フレームの全体を $ONFrame(3)$ とすると、

$\quad ( (e_1, e_2, e_3), (f_1, f_2, f_2)) \in ONFrame(3)\times ONFrame(3)$

$ONFrame(3)\times ONFrame(3)$ には $SO(3)\times SO(3)$ が作用し、この作用は主作用〈principal action〉になるので、この作用のもとで $ONFrame(3)\times ONFrame(3)$ は主等質空間になる。

主等質空間としての $ONFrame(3)\times ONFrame(3)$ を（ネコの）姿勢空間と呼ぶ。ネコの姿勢は $SO(3)\times SO(3)$ -作用で制御可能。

位置空間と主バンドル

$\R^3$ を（ネコの）位置空間と呼ぶ。特定の位置のネコが特定の姿勢をとっている状態の空間は、位置空間×姿勢空間 $\R^3 \times (ONFrame(3)\times ONFrame(3))$ となる。

位置空間への射影 $\pi:\R^3 \times (ONFrame(3)\times ONFrame(3))\to \R^3$ を考えるとファイバーバンドルになる（大域的自明バンドル）。各ファイバーに構造群 $SO(3)\times SO(3)$ が“主に〈principally〉”作用しているから主バンドルになる。

ネコの運動

ネコの位置の変化は写像 $\gamma : [0, a] \to \R^3$ で記述できる。各時点での位置だけでなく姿勢も考えると、 $\tilde{\gamma}:[0, a] \to \R^3\times (ONFrame(3)\times ONFrame(3))$ で記述できる。 $P := \R^3\times (ONFrame(3)\times ONFrame(3))$ として次の可換図式を満たす。

$\require{AMScd} \begin{CD} [0, a] @>{\tilde{\gamma}}>> P\\ @| @VV{\pi}V \\ [0, a] @>{\gamma}>> \R^3 \end{CD}$

もうひとつの主バンドル

使うかどうか分からないが；ひねりの情報を落としたネコの姿勢は2本のベクトル $(e_1, f_1)$ で記述できる。これらは単位ベクトルとしておいたので、 $(e_1, f_1)\in S^1\times S^1$ 。このことから次の写像を作れる。

$\quad ONFrame(3)\times ONFrame(3) \to S^1\times S^1 \\ \quad ( (e_1, e_2, e_3), (f_1, f_2, f_3) ) \mapsto (e_1, f_1)$

$(e_1, f_2)$ を決めると、ひねり（体軸の回りの回転）は $SO(2)\times SO(2)$ なので、上記の写像は構造群 $SO(2)\times SO(2)$ である主バンドルを定義する。

問題における制約

写像 $\tilde{\gamma}:[0, a] \to \R^3\times (ONFrame(3)\times ONFrame(3))$ であって、以下の制約を満たすものが存在すればよい。（位置空間 $\R^3$ は要らないかも知れない。）

$\tilde{\gamma}(0)$ は、逆さまにぶら下げられた状態である。
$\tilde{\gamma}(a)$ は、床にちゃんと着地している。
いくら猫でも無理な姿勢があるだろうから、 $\forall t\in [0, a]$ で、 $\tilde{\gamma}(t)$ は“猫がとり得る姿勢”である。
姿勢の変更は腹筋などで行うのだろうが、この変更（ $SO(3)\times SO(3)$ の作用）も猫が実行可能なものである。
$\forall t\in [0, a]$ で、ニュートン力学の法則を満たしている。