証明図／リーズニング図 (G2 A8)

RSS-G2

※この記事は「記事8」

証明図が描けるようになることは目的にしてないが、特定の典型的例については理解しておいたほうが良いと思うので、2020年2月2日に出した図の詳しい解説をする。例題の図を頑張って丹念に追いかければ、形式化された推論・証明に対して、かなり具体的なイメージを持てるだろう。

演繹システムが行う証明行為とは、データ（主に入れ子のツリー構造）を順番に加工することである。各ステップごとの基本的なデータ加工は、完全に機械的・アルゴリズム的なものである。ステップを積み重ねた全体もまた機械的・アルゴリズム的な行為になる。

演繹システムの（証明成功時の）出力とは、一連のデータ加工のログ〈記録 | 履歴〉である。ユーザーである人間（または他のシステム）は、ログを追いかけて、実行されたデータ加工操作が前もって許されたもの（組み込み、またはユーザーが追加したもの）であるかどうかをチェックできる。

人間でもチェック可能とするには、グラフィカルな分かりやすい表示が必要になる。が、組版・印刷の制約から、十分にグラフィカルにはなってない。極端に省略されたテキストで表現されるのが普通である。

内容：

記法の約束

2020年2月2日に口頭で述べた（愚痴った）ように、「含意'⇒', 伴意'→'」はマズかったかも、と思うけど、「含意'⇒'」を今更変更するのもナンだから、次の約束をする。

  1. 1階のシーケントの矢印〈1階の伴意記号〉は、'-->'（マイナス・マイナス・大なり）にする。
  2. 2階のシーケントの矢印〈2階の伴意記号〉は、'==>'（イコール・イコール・大なり）にする。

'⇒' と '==>' はだいぶ紛らわしいが、注意すれば区別できるだろう。

'⇒'、'-->'、'==>' は、いずれも形式化された表現内で使う記号だが、内容的な意味は次のとおり。

  1. A⇒B ： ￢A∨B と同じ。'⇒'は、短く書くための略記用記号だと思えばよい。
  2. A1, ..., An --> B ： いくつかの論理式 A1, ..., An を仮定すると、 論理式 B を（結論として）推論できる／できた。
  3. K1, ..., Kn ==> J ： いくつかの1階の推論 K1, ..., Kn を認めるなら、1階の推論 J を“推論”できる／できた。

「“推論”」と書いた部分は「2階の推論」のことで、「正しいと認める推論から、正しいと認める推論を導く」規則のこと。これも紛らわしく誤解が生じやすいので、次の約束をする。

  1. 単に「推論」と言ったら「1階の推論」のこと。
  2. 「2階の推論」は「リーズニング」と呼ぶ。
  3. 「推論＝1階の推論」の図を積み重ねた図は証明図
  4. 「リーズニング＝2階の推論」の図を積み重ねた図はリーズニング図

推論〈inference〉と証明〈proof〉の差はあまりない。システム組み込みで、それ以上は（当該システム内では）分解できない証明を「推論」と呼ぶ習慣があるだけ。「推論」の代わりに「組み込み証明」とか「基本証明」とか言ってもよい、つうか、そのほうが整合的。また、必ずしも「組み込み」「基本」でない証明を「推論」と呼ぶこともあるので注意（習慣はとにかくイイカゲンだからね）。

基本的な証明 基本とは限らない証明
1階の 推論, 基本証明 （原則的には）証明
2階の 基本リーズニング リーズニング

「（原則的には）証明」と書いたのは、「推論」と「証明」の区別をたいしてしないこともあるから。

'-->'、'==>' は、本来はメタ記号（メタな記述に使われる記号）ではないのだが、メタ記号に流用されてしまうことが多いし、まー、形式化／メタの境界を曖昧にしてイイカゲンに書くのは便利だったりもする(苦笑)。

  • 論理式単位で入出力・処理するシステム S における証明可能性 A1, ..., An |-S B を、A1, ..., An --> B と書くことがある。
  • シーケント単位で入出力・処理するシステム S' における証明可能性 X1, ..., Xn |-S' Y （X1, ..., Xn, Y は1階のシーケント）を X1, ..., Xn ==> Y と書くことがある。

普通の論理記号（'∧'とか'∀'）でさえ、形式化された記号とメタな記号を区別しない人が多い現状だから、これは致し方ない。文脈により、形式化されているか、メタかを判断する。

形式化された記号とメタな記号の区別を、見た目ですることは無理がある。違いは使い方にあるから。

  • システムへの入力、システムからの出力、システムの内部処理データに使われる記号は形式化された記号である。
  • 人間と人間のコミュニケーションのために、自然言語に混ぜて使われる記号はメタな記号である。

つまり、記号そのものに「形式化／メタ」〈formalized/meta〉の区別があるのではなくて、使う状況で「形式化された記号として使う／メタな記号として使う」の区別が生じる。

例題

Sは、シーケントを入出力と内部データに使う演繹システムとする。単独の論理式 A は入力に使えず、代わりにシーケント T --> A を使うとする。シーケントが形式化された表現であることを強調する目的で "T --> A" のように引用符で囲む（必要があれば、だが）。

  • "A∧B --> C" |-S "T --> A⇒(B⇒C)"

これはメタな記述。まったく同じことを日本語で書き直すなら：

  • シーケント"A∧B --> C"を、事前に（前提として）システムSに記憶させた状態で、シーケント"T --> A⇒(B⇒C)"をターゲット（証明すべきシーケント）として入力すると、Sはターゲットをちゃんと証明する／した。

「ちゃんと証明した」とは、証拠となる証明図（人間が解釈可能なグラフィカルデータ）を出力したこと。シーケントベースのシステムは2階の証明図、すなわちリーズニング図を出力する。そのリーズニング図は次のよう。図が小さいが、後で拡大図を載せる（スマホだと拡大しても厳しいかも）。

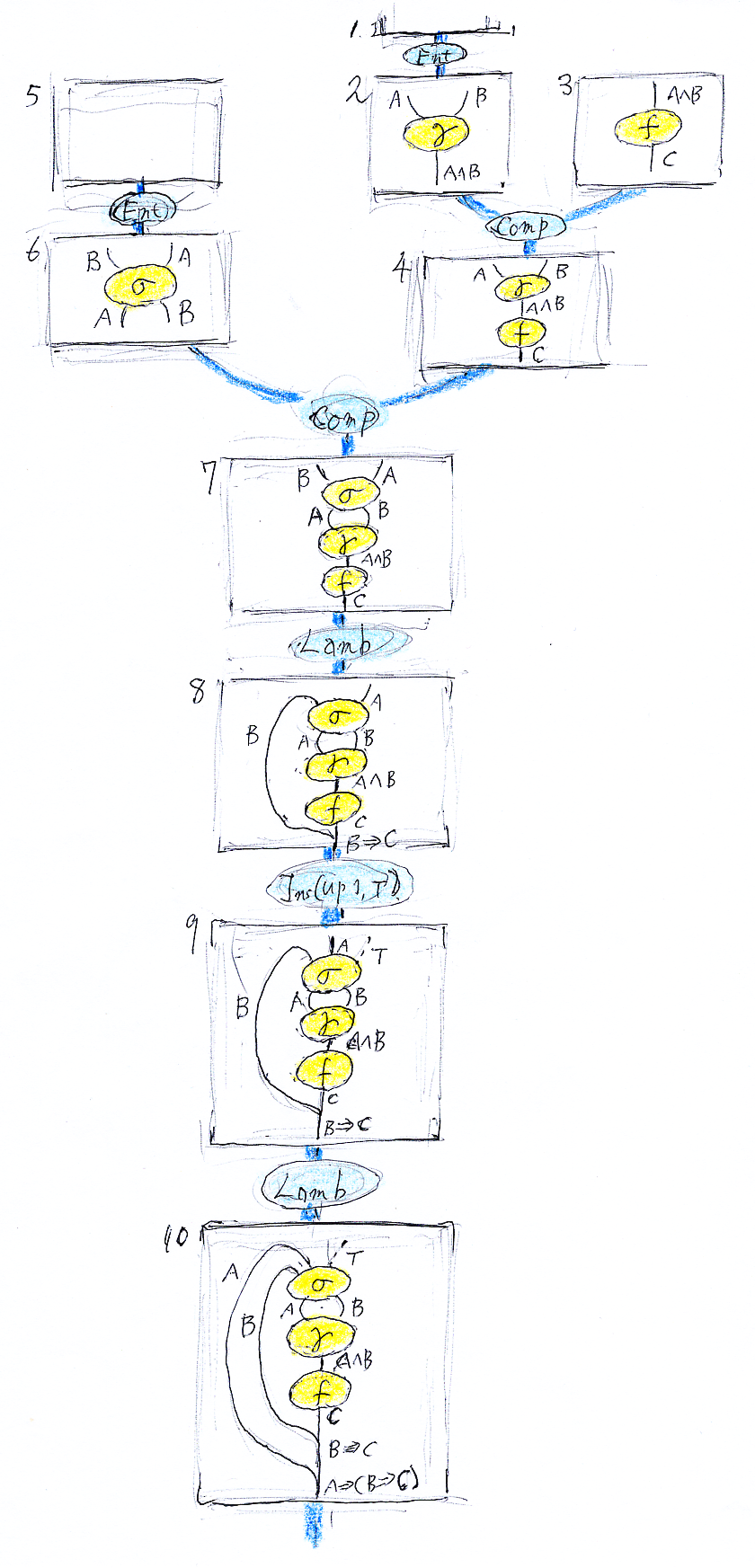
システムSが組み込みで持っている推論（1階の推論）で、図に現れるのは次のとおり（2つだけ）。

  A  B
 ------ σ(並び順の交換)
  B  A


  A  B
 ------ γ(連言導入)
  A∧B

事前に、ユーザーが入力した推論は次。

  A∧B
 ------ f
   C

それぞれを、名前付きシーケント（名前は左端、名前の後にコロン）で書けば：

  • σ:A, B --> B, A
  • γ:A, B --> A∧B
  • f:A∧B --> C

縦書きの推論図、横書きのシーケント、そしてグラフィカルな図は、完全に同じ内容を違う表現法で表したものである。内容的にはまったく同じ！

[補足]
σとγには、A, B を添字で付けるのがより正確である。

  • σA,B:A, B --> B, A
  • γA,B:A, B --> A∧B

また、σA,B:A, B --> B, A における右辺のカンマは、ゲンツェンのLKとは解釈が違う。右辺のカンマも連言〈and〉と解釈する。
[/補足]

基本リーズニングの規則と図

システムが組み込みで持っている基本リーズニング規則〈2階の推論規則〉で、例題の図に登場するのは次のとおり。

  1. Ent〈Enter | 登場 〉 ： 何もない状態から、組み込みの証明図〈推論図〉を出現させる。
  2. Comp〈Composition | 結合〉： 2つの（1階の）証明図を上下にくっつける。
  3. Lamb〈Lambda〉 ： 証明図の最上段の論理式を、最下段に移動して、含意の前件にする。ラムダ計算のラムダ抽象に相当するのでLambda。演繹原理を実現するための操作とも言える。
  4. Ins〈Insert〉 ： 証明図の指定された位置に論理式を挿入する。

これらの基本リーズニングを、シーケントと縦書きのテキストで表現すれば：

     ☆
 ===========Ent
   Γ --> A


  Γ --> Δ  Δ --> B
 =====================Comp
  Γ --> B


  A, Γ --> B
 =============Lamb
  Γ --> A⇒B


  Γ --> A
 =============Ins[up, 0, T]
  T, Γ --> A

説明：

  1. '☆'は「何もない」ことを表す。空な証明図。
  2. Γは論理式のリスト
  3. Insに付いている'up'は最上段の証明図の上側を意味し、0 は左端の位置を示す。最初の論理式の右の位置なら 1。

グラフィカルな表現とテキスト表現

メタな命題 "A∧B --> C" |-S "T --> A⇒(B⇒C)" の証拠となるグラフィカルなリーズニング図〈2階の証明図〉は次（今度は大きい）。

6,4,7,8 の部分だけテキストで書いてみる。

  B A         A  B
 -----σ    -------γ
  A B         A∧B
             ----- f
                C
 =====================Comp
   B A
  -----σ
   A B
  -----γ
   A∧B
  ----- f
    C
 ========Lamb
   [B] A
  -----σ
   A B
  -----γ
   A∧B
  ----- f
    C
  -----
   B⇒C

説明：

  • [B] は、移動した跡を示す。実際には、ここにあった B は、最下段の含意前件（左側）に移動している。Lambの効果をリアルに再現するには、Bをホントに移動して見せるアニメーションが適切。

[追記]
試しに、上の縦書きリーズニング図で出てくる最初の Comp を横書きしてみる。

      σ:B,A→A,B
Comp::                        ==> σ:B,A→A,B; γ:A,B→A∧B; f:A∧B→C
      γ:A,B→A∧B; f:A∧B→C

Comp操作の上段の左右を右側の上下に、Compの入出力の上下配置を左右配置に変更した。さらに、左側の上下も左右に潰すと：

Comp::(σ:B,A→A,B), (γ:A,B→A∧B; f:A∧B→C) ==> σ:B,A→A,B; γ:A,B→A∧B; f:A∧B→C

単に、書き方における 上下←→左右 の入れ替えに過ぎない。こういうクダラナイとも言える書き方のドタバタに付き合わされるのはバカバカしいのだが、組版・印刷というユーザーインターフェースの制約内での伝達の苦労と工夫の結果。現状では、このテの苦労と工夫に付き合って、書き換え練習をするしかない。
[/追記]

全部をテキストで書くのは大変なので、1階の証明図の仮定と結論だけ抜き出してシーケントにすると：

  B, A --> A, B    A, B --> C
 =============================Comp
  B, A --> C
 ============Lamb
  A --> B⇒C

格段に短くなる。さらに、横線を二重線（イコールの繰り返し）で書くのもやめて、リーズニングの名前も省略：

  B, A --> A, B    A, B --> C
 -----------------------------
  B, A --> C
 ------------
  A --> B⇒C

実際に使われるのはこの形。生の正確なログ〈記録 | 履歴〉は膨大になるので、省略に省略を重ねてコンパクトに書くようにしている。

縦書きの証明図の仮定と結論を横書きにするのに '-->' を使ったのと同様に、上記の縦書きリーズニング図〈2階の証明図〉の仮定（上段のシーケント）と結論（下段のシーケント）を抜き出して横書きにするのに '==>' を使えば：

  • (B, A --> A, B), (A, B --> C) ==> (A --> B⇒C)

このような2階のシーケントをデータとして加工する演繹システムもあるが、古典論理の形式的証明では、1階のシーケントの加工で間に合う。

実際に使われる表現・表示の方法

例題のグラフィカル表現のような絵を描くのは僕（檜山）くらいで、ほとんど誰も描かない。実際に使われる表現・表示の方法は：

  1. 最後の証明図、例でいえば 10 の証明図だけを提示する。
  2. 前節で述べた方法でシーケントの証明図を提示する。

10 の証明図だけを提示（使った規則は省略）：

         T
 [B] [A]
 -------
  A  B
 ------
  A∧B
 ------
   C
 ------
  B⇒C
 ----------
  A⇒(B⇒C)

シーケントの証明図を提示：

                     ☆
              ----------------
      ☆        A, B --> A∧B    A∧B --> C
 ------------   ---------------------------
 B, A --> A, B     A,B --> C
 ----------------------------
    B, A --> C
  --------------
     A --> B⇒C
  --------------
   A,T --> B⇒C
  -----------------
    T --> A⇒(B⇒C)

慣れれば、省略されている様々な情報を自力で補完できるが、あまりにも省略し過ぎだと思いませんか？

モノイドやモノイド圏の指標 補足解説

説明 その他

参照のためにコピーした（わずかに変更）。

「マイクロコスモ原理と構造の無限タワー」に補足。記法を少し改善する。

「掛け算」「乗法」「積」などと呼ばれる演算の中置記法で使われる記号は色々ある。

  1. なし（単なる併置）
  2. ×
  3. ・
  4. \otimes
  5. 他にも色々

記号を修飾する方法は、

  1. 太字
  2. 斜体
  3. ダッシュ（プライム）
  4. 下線
  5. 上線
  6. ハット
  7. 他にも色々

色々な種類・装飾を使うのは、概念的区別をするため。これからやることは、できるだけ種類・装飾を使わないようにすること。代わりに、次元と呼ばれる番号（整数値）で識別する。

異なる次元の同じ記号を同時に使うときだけ装飾による区別が必要。僕は主に太字を使ってきたがダッシュ（'）にする。書くのが簡単。もっと重要な理由は、a, a', a'', a''' のような書き方が出来ること。“太字の太字”は、普通は出来ない。

次元nのモノ達に注目して語っている文脈で、次元(n+1)の記号が出てきたらダッシュを1つ付ける。次元(n+2)の記号にはダッシュを2つ付ける。以下同様。

これからは、「掛け算」「乗法」「積」を一律に大文字Yで表記する。Yを使う理由は象形文字としてだ。「マックレーンの五角形をインデックスなしの等式で表す」を見ればYをつかう理由がわかるだろう。

ツリー状図の合流点のイメージからY。

他に単位対象と恒等（恒等写像、恒等射、恒等関手、恒等自然変換など）を表す文字が必要だが、「マックレーンの五角形をインデックスなしの等式で表す」では 単位対象＝i, 恒等＝I としていた。象形文字としてはこれが使いやすい。

が、「マイクロコスモ原理と構造の無限タワー」では行きがかり上、単位（対象／射）をIとしている。恒等がJになっている。しかも、Iが単位対象（0-射）と単位ポインティング射（1-射）の2つの意味でオーバーロードされている。

次が、辻褄が合っていて象形文字として使いやすい。

記号 意味
U 台対象
Y 掛け算、乗法、積
1 単位対象
i 単位射
I 恒等

だがこれも、1, i, I がとても紛らわしいという欠点がある。目を凝らして注意すべし！ それと、次の点に注意しよう。

  • i:1'→U
  • i0(0) = 1 ∈ |U| （0は自明圏の唯一対象）

n次元の自明圏からのn次元の単位射（単位写像、単位関手、単位自然変換かも知れない）iの0-部分〈対象部分 | object part〉に自明対象（自明圏の唯一の0-射、自明アトム）を入れた値が(n-1)次元の単位対象。神経質に気にする必要はないが、一般に、モノイド圏や高次圏の単位の仲間（恒等、モノイド単位、ポインティング射、終対象など）は難しい → 「モノイド圏の単位対象の定義について： これ難しいやん」参照。

「マイクロコスモ原理と構造の無限タワー」に出てきた指標を、上記の象形文字に置き換えてみる。

1-signature 1-mon := {
 0-morphism U;
 1-morphism m:U\otimesU→U;
 1-morphism i:I→U;
}

\otimes → Y と置き換えたいのだが、それだと m → Y と区別がつかないので、\otimes → Y' とする。

  • U → U（変化なし）
  • m → Y
  • \otimes → 中置から前置のY'
  • i → i（変化なし）
  • I → 1'（イチ・ダッシュ）

中置から前置に切り替えるので、

  • U\otimesU → Y'(U, U)

実は、(U, U) というペアを作るためにデカルト構造が必要だったりするのだが、そこまで詮索しないことにする。（← ここが気になる人がいるのかな？ だとしたらその疑問は本質を突いている、鋭い。）

んで、書き換えると：

1-signature 1-mon := {
 0-morphism U;
 1-morphism Y:Y'(U, U)→U;
 1-morphism i:1'→U;
}

Y'と1'が１次元上からやって来ている。

次にモノイド圏の指標。

2-signature 2-mon := {
 0-morphism U;
 1-morphism Y = \otimes:U×U→U;
 1-morphism I:I→U;
 1-morphism J = IdU:U→U;
 2-morphism α::(Y×J)*Y⇒αU,U,U*(J×Y)*Y:(U×U)×U→U;
 2-morphism λ::(I×J)*Y⇒λU:I×U→U;
 2-morphism ρ::(J×I)*Y⇒ρU:U×I→U;
}

記号の種類・装飾のバラエティを取り除く。

書き換え前 書き換え後
U U
\otimes Y
× Y'
I i
I 1'
J I
* #（下添字略）
αU,U,U α'（下添字略）
λU λ'（下添字略）
ρU ρ'（下添字略） 
2-signature 2-mon := {
 0-morphism U;
 1-morphism Y: Y'(U, U)→U;
 1-morphism i:1'→U;
 1-morphism I:U→U;
 2-morphism α:: Y'(Y, I)#Y⇒α'# Y'(I, Y)#Y:  Y'(Y'(U, U), U)→U;
 2-morphism λ:: Y'(i, I)#Y⇒λ': Y'(1', U)→U;
 2-morphism ρ:: Y'(I, i)#Y⇒ρ': Y'(U, 1')→U;
}

Y', 1', α', λ', ρ' が１次元上から来ている記号。絵で描くときは：

記号 描き方
U 描かない
Y Yの形
Y' 併置のあいだの空白
i iの形かその変形
1' 点線か空白
I Iの形、ワイヤー
# 上下の併置（スタッキング）
α' ワイヤーの位置ずらし
λ' 点線（左）と実線（ワイヤー）の合流
ρ' 点線（右）と実線（ワイヤー）の合流

絵の基本は、「圏論の随伴をちゃんと抑えよう： お絵描き完全解説 - 檜山正幸のキマイラ飼育記 (はてなBlog)」とか。絵を描いてみるのはおススメ。テキスト記号だけだと、なかなか事情が分からないから。

記号・記法の約束 20200118

その他
  • この記事のURL： https://m-hiyama-second.hatenablog.com/entry/2020/01/18/151235
  • ローカルファイル： YK-*/Notations2020.txt

\newcommand{\hyph}{\mbox{-}} \newcommand{\vvec}[1]{{#1}\!\!\downarrow}
内容：

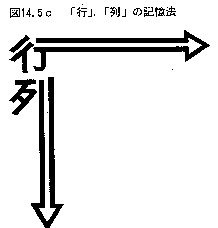
行列の記法

成分〈要素 | 項目 | 係数〉が集合Sの要素で、サイズがm行n列の行列の全体を Mat[S](n, m) と書く（n, mの順序に注意）。Mat[S](n, m) を S[{}^m_n] とも書く。特に、

  • S[{}^n_1] = Mat[S](1, n) 縦タプル
  • S[{}^1_n] = Mat[S](n, 1) 横タプル

S[{}^n_1] の要素を成分表示するときは、縦並び上付き添字にする。添字〈インデックス番号〉は上から下に向かって増える。

  • x = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in S[^n_1]

S[{}^1_n] の要素を成分表示するときは、横並び下付き添字にする。添字〈インデックス番号〉は左から右に向かって増える。

  • x = \begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix} \in S[_n^1]

縦並びと横並びを区別するために、次のような注釈的飾り記号（矢印）を付けることがある。が、いつでも付けるとは限らない。（むしろ、たいていは付けない。）

  • 縦並び \vvec{x}
  • 横並び \vec{x}

つまり、

x = \vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in S[^n_1] \\ \:\\ x = \vec{x} = \begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix} \in S[_n^1]

\vvec{x} は、世間ではほとんど使われてないので注意。縦でも横でも \vec{x} で書くのが習慣。

多くの場合、成分の集合はR（実数）なので、{\bf R}[{}^m_n] を考える。

点とベクトルの区別

点の座標とベクトルの成分表示は、見た目で区別できない。区別したいときは、

  • 点： x = (x_1, x_2, \cdots, x_n)
  • ベクトル： \vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix}

縦タプルを横書きで書きたいときは、

  • x = \vvec{x} = [x^1, x^2, \cdots, x^n]^T

Tは、transpose〈転置〉の't'から。

図形的な矢線ベクトルの成分表示は、原則として縦タプルを使う。

集合 Rn が、点の座標の集合か、ベクトルの成分表示の集合かをどうしても区別したいときは、

  • 点： {\bf R}^n
  • ベクトル： \vvec{{\bf R}^n} = {\bf R}[^n_1]

つまり、

  • 点： x = (x_1, x_2, \cdots, x_n) \in {\bf R}^n
  • ベクトル： x = \vvec{x} = \begin{bmatrix}x^1 \\ x^2 \\ \vdots \\ x^n \end{bmatrix} \in \vvec{{\bf R}^n}
内積と行列の掛け算

高校教科書で使われている「内積にドット」は使わない。ドットはスカラーや行列の掛け算記号に使う。

  • 内積： (x|y)
  • 掛け算（スカラー乗法〈倍〉、スカラー／行列の積）： x・y

掛け算記号の省略

  1. スカラー・スカラー は多くの場合省略される。
  2. スカラー・ベクトル、ベクトル・スカラー は多くの場合省略される。
  3. 行列・行列 は多くの場合省略される。が、付けるときはドット。
  4. 内積と外積（外積は ^ または ×）は省略しない。

無闇に省略しすぎるとワケワカラナクなるので、演算子記号はある程度は付けたほうがよい。

行列の成分表示

縦方向に変化する添字〈インデックス〉は上付き、横方向に変化する添字〈インデックス〉は下付き。

\begin{bmatrix} a^1_1 & a^1_2 & \ldots & a^1_n \\ \vdots & \vdots & \ddots & \vdots \\ a^m_1 & a^m_2 & \ldots & a^m_n \\ \end{bmatrix}

次のような規則を設ける人もいるが、我々は守らない（どうせ守れないから）。文字の使用法は自由である。

  • 行列は大文字、縦タプルは小文字、横タプルはギリシャ文字小文字 （守らない！）
  • 行列は大文字、その成分は小文字 （無視！）

太字（ボールド体）、上に矢印などの書体・文字修飾も原則として使わない（気まぐれでたまに使うが）。

行列のサイズ

行列の行方向と列方向を憶えるには、「はじめての圏論 その第2歩：行列の圏 - 檜山正幸のキマイラ飼育記 (はてなBlog)」 に載せた次の絵：

Aが行列のとき：

  • width(A) = Aの横幅 = Aの列数
  • height(A) = Aの縦高さ = Aの行数

「n×m 行列」という書き方は、列数〈幅〉・行数〈高さ〉がハッキリしないので、「n列m行 行列」または「m行n列 行列」を使う。

1行1列の行列とスカラーは区別する必要はない。（稀に区別することもあるが。）

行列の等しさ

スカラーの等しさは分かっているとして、行列の等しさ A = B は次のように定義する。

  1. A と B のサイズは同じ（列数が同じ かつ 行数が同じ）
  2. すべて i, j に対して A_i^j = B_i^j

AもBもn列m行だとすれば：

  • A_i^j = B_i^j \:\:\:(1 \le i \le n,\: 1 \le j \le m)

特に、縦タプルの等しさ x = y は：

  • x^i = y^i \:\:\: (1 \le i \le n)

横タプルの等しさ x = y は：

  • x_i = y_i \:\:\: (1 \le i \le n)
行列の和と積の成分表示

和：

  • (A + B)_i^j = A_i^j + B_i^j

特に、縦タプルと横タプルの和は：

  • (x + y)^i = x^i + y^i
  • (x + y)_i = x_i + y_i

積；

  • (BA)_i^k = {\displaystyle \sum_{j = 1}^m} B_j^k A_i^j
総和の性質

X, Y などは有限集合（リストだと思ってよい）で、f, g などは有限集合から実数への関数を表す。

  1. \displaystyle \sum_{x\in X}(f(x) + g(x)) = \sum_{x\in X}f(x) + \sum_{x\in X}g(x) \\
  2. \displaystyle a\left(\sum_{x\in X}f(x)\right) = \sum_{x\in X}a f(x) \\
  3. \displaystyle \left( \sum_{x\in X}f(x) \right)\left( \sum_{y\in Y} g(y)\right) = \sum_{x\in X} \sum_{y\in Y} f(x)g(y) = \sum_{(x, y)\in X\times Y} f(x)g(y)\\
  4. \displaystyle \sum_{z \in X + Y}f(z) = \sum_{z \in X}f(z) + \sum_{z \in Y}f(z) \\
  5. \displaystyle \sum_{(x, y) \in X \times Y}f(x, y) = \sum_{x \in X}\sum_{y \in Y}f(x, y) = \sum_{y \in Y}\sum_{x \in X}f(x, y) \\
// 1 左辺
var sum = 0;
for (x in  X) {
  sum += (f(x) + g(x));
}
return sum;
// 1 右辺
var sum = 0;
for (x in  X) {
  sum += f(x);
}
for (x in  X) {
  sum += g(x);
}
return sum;

// 2 左辺
var sum = 0;
for (x in  X) {
  sum += f(x);
}
return a*sum;
// 2 右辺
var sum = 0;
for (x in  X) {
  sum += a*f(x);
}
return sum;

// 3 左辺
var sum_f = 0;
for (x in  X) {
  sum_f += f(x);
}
var sum_g = 0;
for (y in  Y) {
  sum_g += g(y);
}
return sum_f * sum_g;
// 3 右辺 1
var sum = 0;
for (x in  X) {
  for (y in Y) {
    sum += f(x)*g(y);
  }
}
return sum;
// 3 右辺 2
var sum = 0;
for (y in  Y) {
  for (x in X) {
    sum += f(x)*g(y);
  }
}
return sum;

// 4 左辺
var sum = 0;
for (z in  X + Y) {
  sum += f(z);
}
return sum;
// 4 右辺
var sum = 0;
for (z in  X) {
  sum += f(z);
}
for (z in  Y) {
  sum += f(z);
}
return sum;

// 5 左辺
var sum = 0;
for ([x, y] in X*Y) {
  sum += f([x, y]);
}
return sum;
// 5 右辺 1
var sum = 0;
for (x in X) {
  for (y in Y) {
    sum += f([x, y]);
  }
}
return sum;
// 5 右辺 2
var sum = 0;
for (y in Y) {
  for (x in X) {
    sum += f([x, y]);
  }
}
return sum;

モノイド閉圏の事例： オシマイ

その他 特例

これでオシマイにします。シリーズ記事をすべてリストしたい場合は、「モノイド閉圏の事例：」で検索すればいいでしょう。

記事の推敲・リライト、再編成などは（当初は多少やるつもりでいたが）やる気はありません。明らかな間違い（誤字・脱字含む）の訂正以外は、もう変更はないでしょう。

やった計算／やってない計算のリストは次にあります。

「*」付きは計算をやらなくても理論的に出ます。△は、ほんとはやるべきだが省略した計算です。

概念的な話は：

  1. ラムダ計算の自然性とお絵描き
  2. モノイド閉圏： カリー化からニョロニョロまで

本論と関係はないけど、計算作業は単純肉体労働に近いってことに関連して：

モノイド閉圏の事例： ボックス積の双関手性

その他 特例

ボックス積 (-□-) を Box:SG×SG→SG とも書く。ボックス積が双関手性を持つとは、直積圏からの関手であることだから：

  1. Box( (f, f');(g, g') ) = Box( (f, f') );Box( (g, g') ) （結合の保存）
  2. Box( (A, B)^ ) = Box( (A, B) )^ （単位の保存）

中置演算子形式ならば：

  1. (f;g)□(f';g') = (f□f');(g□g') （交替律）
  2. A^□B^ = (A□B)^ （単位の交替律）

これらを計算により直接示す。

(f;g)□(f';g') = (f□f');(g□g')
  • f:A→B, g:B→C, f;g:A→C
  • f':A'→B', g':B'→C', f';g':A'→C'
  • (f;g)□(f';g'):A□A'→C□C'

とする。

左辺 : A□A'→C□C'
=
[
  λ0(a, a')∈A□A'.(
    ( (f;g)(a), (f';g')(a') ) ∈C□C'
  )
  ALSO
  λ1(a→a', a'')∈A□A'.(
    ( (f;g)(a→a'), (f';g')(a'') ) ∈C□C'
  )
  OR
  λ1(a, a'→a'')∈A□A'.(
    ( (f;g)(a), (f';g')(a→a'') ) ∈C□C'
  )
] : A□A'→C□C'

右辺 : A□A'→C□C'
= 
[
  λ0(a, a')∈A□A'.(
    ( f(a), f'(a') ) ∈B□B'
  )
  ALSO
  λ1(a→a', a'')∈A□A'.(
    ( f(a→a'), f'(a'') ) ∈B□B'
  )
  OR
  λ1(a, a'→a'')∈A□A'.(
    ( f(a), f'(a'→a'') ) ∈B□B'
  )
] ; [
  λ0(b, b')∈B□B'.(
    ( g(b), g'(b') ) ∈C□C'
  )
  ALSO
  λ1(b→b', b'')∈B□B'.(
    ( g(b→b'), g'(b'') ) ∈C□C'
  )
  OR
  λ1(b, b'→b'')∈B□B'.(
    ( g(a), g'(b'→b'') ) ∈C□C'
  )
] : A□A'→C□C'
= 
[
  λ0(a, a')∈A□A'.(
    ( (f;g)(a), (f';g')(a') ) ∈C□C'
  )
  ALSO
  λ1(a→a', a'')∈A□A'.(
    ( (f;g)(a→a'), (f';g')(a'') ) ∈C□C'
  )
  OR
  λ1(a, a'→a'')∈A□A'.(
    ( (f;g)(a), (f';g')(a'→a'') ) ∈C□C'
  )
] : A□A'→C□C'
A^□B^ = (A□B)^
左辺 :A□B→A□B
= A^□B^
=
[
  λ0(a, b)∈A□B.(
    (a, b) ∈A□B
   )
   ALSO
  λ1(a→a', b)∈A□B.(
    (a→a', b) ∈A□B
   )
   OR
  λ1(a, b→b')∈A□B.(
    (a, b→b') ∈A□B
   )
] :A□B→A□B

右辺も同じ表示になることは自明だろう。

モノイド閉圏の事例： ベータ変換等式

その他 特例
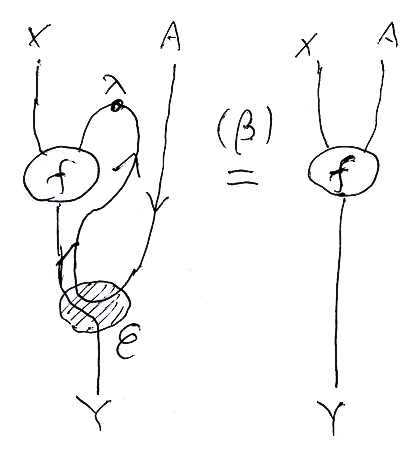
  • (ΦX,A,Y(f)□A^);ev = f \newcommand{\For}{\mbox{For}\:\:}\newcommand{\cat}[1]{{\mathcal {#1}}} \newcommand{\id}{\mbox{id}}

\For f : X\otimes A \to Y \:\mbox{in}\: \cat{C},\\ (\Lambda^{X,A}_Y(f)\otimes \id_A);{^A ev_X} = f

ΦX,A,Y(f) = Φ(f) = F と置いて、(ΦX,A,Y(f)□A^) = F□A^ を計算する。

F□A^ : X□A→hom(A, Y)□A
=
[
  λ0(x, a)∈A□A.(
     (F(x), a) ∈hom(A, Y)□A
  )
  ALSO
  λ1(x→x', a)∈A□A.(
     (F(x→x'), a) ∈hom(A, Y)□A
  )
  OR
  λ1(x, a→a')∈A□A.(
     (F(x), a→a') ∈hom(A, Y)□A
  )
] : X□A→hom(A, Y)□A
=
λ[(x, a) ALSO (x→x', a) OR (x, a→a')∈X□A.(
  [
   ( (F(x), a) ∈hom(A, Y)□A)
   ALSO
   ( (F(x→x'), a) ∈hom(A, Y)□A)
   OR
   ( (F(x), a→a') ∈hom(A, Y)□A)
  ] ∈hom(A, Y)□A
)

これに ev〈エバル | 評価射〉を後結合すると、

λ[(x, a) ALSO (x→x', a) OR (x, a→a')∈X□A.(
  [
   ( F(x)(a) ∈Y)
   ALSO
   ( (F(x→x')(a) ∈Y)
   OR
   ( (F(x)(a→a') ∈Y)
  ] ∈Y
)

という写像になる。F = Φ(f) だったので、これは f に他ならない。したがって、

  • (ΦX,A,Y(f)□A^);ev = f

が成立する。

モノイド閉圏の事例： 反カリー化

その他 特例

反カリー化を定義して、カリー化の逆写像であることを計算で直接的に示してみる。

念のために、カリー化の定義を再掲：

ΦA,B,C : Hom(A□B, C)→Hom(A, hom(B, C)) :=
  λf∈Hom(A□B, C).(
    [
     λ0a∈A.(
        [λ0b∈B.( f(a, b) ∈C)
         ALSO
         λ1b→b'∈B.( f(a, b→b') ∈C)
        ] ∈hom(B, C)
     )
     ALSO
     λ1a→a'∈A.(
       [λ01b∈B.( f(a→a', b) ∈C)] ∈hom(B, C)
     )
    ] ∈Hom(A, hom(B, C))
  )
反カリー化の定義：
ΨA,B,C : Hom(A, hom(B, C))→Hom(A□B, C) :=
  λF∈Hom(A, hom(B, C)).(
    [
     λ0(a, b)∈A□B.(
         F(a)(b) ∈C
      )
     ALSO
     λ1(a→a', b)∈A□B.(
         F(a→a')(b) ∈C
      )
      OR
     λ1(a, b→b')∈A□B.(
         F(a)(b→b') ∈C
      )
    ] ∈Hom(A□B, C)
  )
Φ;Ψ :Hom(A□B, C)→Hom(A□B, C) の計算：

f∈Hom(A□B, C) に対して、(Φ;Ψ)(f) = (Ψ\circΦ)(f) = Ψ(Φ(f)) を計算する。Φ(f) = F : A→hom(B, C) と置く。

Ψ(F) : A□B→C
=
[
 λ0(a, b)∈A□B.(
     F(a)(b) ∈C
  )
 ALSO
 λ1(a→a', b)∈A□B.(
     F(a→a')(b) ∈C
  )
  OR
 λ1(a, b→b')∈A□B.(
     F(a)(b→b') ∈C
  )
] : A□B→C
=
[
 λ0(a, b)∈A□B.(
     f(a, b) ∈C
  )
 ALSO
 λ1(a→a', b)∈A□B.(
     f(a→a', b) ∈C
  )
  OR
 λ1(a, b→b')∈A□B.(
     f(a, b→b') ∈C
  )
]
= f

したがって、

  • Φ;Ψ = idHom(A□B, C)
Ψ;Φ :Hom(A, hom(B, C))→Hom(A, hom(B, C)) の計算：

F∈Hom(A, hom(B, C)) に対して、(Ψ;Φ)(F) = (Φ\circΨ)(F) = Φ(Ψ(F)) を計算する。Ψ(F) = f : A□B→C と置く。

Φ(f) : A→hom(B, C)
=
[
 λ0a∈A.(
    [λ0b∈B.( f(a, b) ∈C)
     ALSO
     λ1b→b'∈B.( f(a, b→b') ∈C)
    ] ∈hom(B, C)
 )
 ALSO
 λ1a→a'∈A.(
   [λ01b∈B.( f(a→a', b) ∈C)] ∈hom(B, C)
 )
] : A→hom(B, C)
=
[
 λ0a∈A.(
    [λ0b∈B.( F(a)(b) ∈C)
     ALSO
     λ1b→b'∈B.( F(a)(b→b') ∈C)
    ] ∈hom(B, C)
 )
 ALSO
 λ1a→a'∈A.(
   [λ01b∈B.( F(a→a')(b) ∈C)] ∈hom(B, C)
 )
] : A→hom(B, C)

最後の式が F :A→hom(B, C) に等しいためには、次が必要になる。

λ0a∈A.(
   [λ0b∈B.( F(a)(b) ∈C)
    ALSO
    λ1b→b'∈B.( F(a)(b→b') ∈C)
   ] ∈hom(B, C)
)
= F(0) : A(0)→Hom(B, C)



λ1a→a'∈A.(
  [λ01b∈B.( F(a→a')(b) ∈C)] ∈hom(B, C)
)
= F(1) : A(1)→Defm(B, C)

これらは定義から容易に確認できる（割愛）。

したがって、

  • Ψ;Φ = idHom(A, hom(B, C))

モノイド閉圏の事例： 計算の方法に関して

その他 特例

ここまで計算してきて感じたこと：

  1. 図（ストリング図）のワイヤーにラベルがないのは分かりにくい。横着せずにワイヤーにラベル（対象の名前）を書いたほうがいい。悪い例は↓
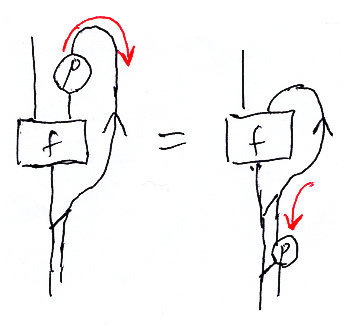
  2. 写像ブロックとデータブロックを区別して書く必要はないかも。「写像ブロック←→データブロック」の入れ替えをよくするので、括弧の書き換えがめんどくさい。どちらも角括弧でいいと思う。
  3. 写像ブロックとデータブロックを統合するなら、セマンティクスも統合したほうがいいだろう。ブロックベースのラムダ計算を構成することになる。
  4. データブロックをひとつの変数で表すブロック変数は便利。ラムダ変数や代入計算の変数にブロック変数が使える。

ブロックベースのラムダ計算を作るなら、次のモノを扱うことになる。

  1. 成分〈コンポーネント〉： 頂点、辺、準同型写像、準同型写像の成分、変形
  2. ALSOペア ： ALSOで区切った2成分ブロック
  3. ALSO-ORトリプル ： OLSOとORで区切った3成分ブロック

まー、今後使う予定はないから、これから計算デバイスを改良する気力はわかないけど。

モノイド閉圏の事例： カリー化の自然性 (続き2)

その他 特例

前の記事の続き。後でひとつの記事にまとめるかも。

真っすぐなスライディング
  • ΦX,A,Y'( f;q ) = ΦX,A,Y(f);hom(A, q) : X→hom(A,Y')

左辺：

Φ( f;q )  : X→hom(A,Y')
=
[
  λ0x∈X.(
    [
      λ0a∈A.( q(f(x, a)) ∈Y')
      ALSO
      λ1a→a'∈A.( q(f(x, a→a')) ∈Y')
    ]  ∈Hom(X, Y')
   )
   ALSO
   λx→x'∈X.(
     [
       λ01a∈A.( q(f(x→x', a)) ∈Y')
     ] ∈Defm(A, Y')
    )
] ∈Hom(X, hom(A, Y'))
=
λ{x ALSO x→x'}∈X.(
 {
    [
      λ0a∈A.( q(f(x, a)) ∈Y')
      ALSO
      λ1a→a'∈A.( q(f(x, a→a')) ∈Y')
    ]  ∈Hom(X, Y')
    ALSO
    [
      λ01a∈A.( q(f(x→x', a)) ∈Y')
    ] ∈Defm(A, Y')
 }
)

準備：

Φ(f) : X→hom(A, Y)
=
[
  λ0x∈X.(
    [
      λ0a∈A.( f(x, a) ∈Y)
      ALSO
      λ1a→a'∈A.( f(x, a→a') ∈Y)
    ]  ∈Hom(A, Y)
   )
   ALSO
   λx→x'∈X.(
     [
       λ01a∈A.( f(x→x', a) ∈Y)
     ] ∈Defm(A, Y)
    )
] ∈Hom(X, hom(A, Y))
=
λ{x ALSO x→x'}∈X.(
 {
   [
     λ0a∈A.( f(x, a) ∈Y)
     ALSO
     λ1a→a'∈A.( f(x, a→a') ∈Y)
   ]  ∈Hom(X, Y)
   ALSO
   [
     λ01a∈A.( f(x→x', a) ∈Y)
   ] ∈Defm(A, Y)
 } ∈Hom(X, hom(A, Y))
)



hom(A, q:Y→Y') :hom(A, Y)→hom(A, Y')
=
[
  λ0u∈hom(A, Y).( u;q ∈Hom(A, Y) )
  ALSO
  λ1u⇒v∈hom(A, Y).( (u⇒v);;q  ∈Defm(A, Y) )
]
=
λ{u ALSO u⇒v}∈hom(A, Y).(
 {
   ( u;q ∈Hom(A, Y))
    ALSO
   ( (u⇒v);;q ∈Defm(A, Y))
 }
)



右辺  : X→hom(A,Y')
=
Φ(f);hom(A, q)
=
λ{x ALSO x→x'}∈X./(
 {
   ( u;q ∈Hom(A, Y'))
    ALSO
   ( (u⇒v);;q ∈Defm(A, Y'))
  }
  /
  {u ALSO u⇒v} = Φ(f)({x ALSO x→x'})
)/
=
λ{x ALSO x→x'}∈X.(
 {
   ( Φ(f)(x);q ∈Hom(A, Y'))
    ALSO
   ( (Φ(f)(x)⇒Φ(x)(v));;q ∈Defm(A, Y'))
  }
)

左辺と右辺を比べてみる：

左辺 : X→hom(A,Y') =
λ{x ALSO x→x'}∈X.(
 {
    [
      λ0a∈A.( q(f(x, a)) ∈Y')
      ALSO
      λ1a→a'∈A.( q(f(x, a→a')) ∈Y')
    ]  ∈Hom(A, Y')
    ALSO
    [
      λ01a∈A.( q(f(x→x', a)) ∈Y')
    ] ∈Defm(A, Y')
 }
)

右辺 : X→hom(A,Y') =
λ{x ALSO x→x'}∈X.(
 {
   ( Φ(f)(x);q ∈Hom(A, Y'))
    ALSO
   ( (Φ(f)(x)⇒Φ(x)(v));;q ∈Defm(A, Y'))
  }
)

等式を示すには、次をターゲット（証明の目標）にすればよい。

[
   λ0a∈A.( q(f(x, a)) ∈Y')
   ALSO
   λ1a→a'∈A.( q(f(x, a→a')) ∈Y')
]  ∈Hom(A, Y')
=
( Φ(f)(x);q ∈Hom(A, Y'))



[
 λ01a∈A.( q(f(x→x', a)) ∈Y')
] ∈Defm(A, Y')
=
( (Φ(f)(x)⇒Φ(x)(v));;q ∈Defm(A, Y'))

この2つの等式は、Φ〈カリー化〉の定義／;〈写像の結合〉の定義／;;〈変形と写像の結合〉の定義から出るので、計算は割愛する。