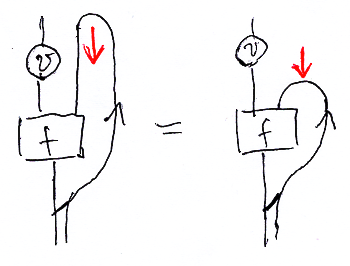
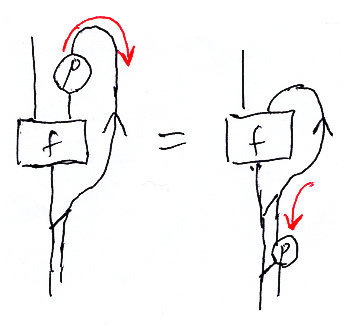
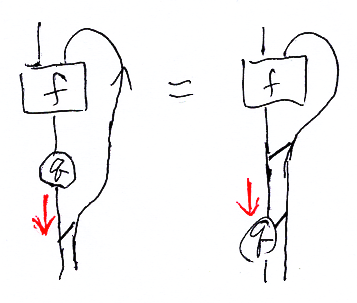
記号の乱用
f(0)もf(1)も区別せずに単にfと書くことが多い。f(0) から f(1) が決まってしまうので、乱用しても弊害は少ないと思われる。
- For f:A→B in SG
- f(s(i)) = s(f(i))
- f(t(i)) = t(f(i))
- i∈A(a, b) ⇒ f(i)∈B(f(a), f(b))
文字の使い方の目安
あくまで目安。守らないことも、変更することもあり得る。
| 文字 |
種別 |
用途・意味 |
備考 |
| a, b, c, d |
変数 |
グラフの頂点 |
a', b' なども |
| f, g, h |
変数 |
グラフ射 |
SGの射、ホムグラフの頂点 |
| i, j, k |
変数 |
グラフの辺 |
あまり使わない |
| s, t |
構成素名 |
辺の始点と終点 |
|
| u, v, w |
変数 |
グラフ射 |
主にホムグラフの頂点 |
| x, y, z |
変数 |
グラフの頂点 |
x', y' なども |
| A, B, C, D |
変数 |
単純グラフ |
SGの対象 |
| F, G |
変数 |
ホムグラフへのグラフ射 |
高階グラフ射 |
| 1 |
固有名 |
単頂点離散グラフ |
太字のイチ |
| X, Y, Z |
変数 |
単純グラフ |
SGの対象 |
| α, β, γ |
変数 |
変形 |
ホムグラフの辺 |
| γ |
構成素名 |
内部結合 |
変数とかぶり |
| α |
構成素名 |
結合律子 |
変数とかぶり |
| ε |
構成素名 |
随伴の余単位 |
ev とも書く |
| η |
構成素名 |
随伴の単位 |
ins とも書く |
| φ |
構成素名 |
内部カリー化 |
ホムグラフ間の射 |
| ψ |
構成素名 |
内部反カリー化 |
ホムグラフ間の射 |
| λ |
構成素名 |
左単位律子 |
|
| λ |
メタ記号 |
ラムダ記号 |
左単位律子とかぶり |
| ρ |
構成素名 |
右単位律子 |
|
| σ |
構成素名 |
対称〈スワップ〉 |
|
| ι |
構成素名 |
内部恒等 |
|
| Φ |
構成素名 |
{右}?カリー化 |
ホムセット間写像、通常はΛ |
| Ψ |
構成素名 |
反{右}?カリー化 |
ホムセット間写像、通常はΓ |
グラフ射を部分に分ける
f:A→B in SG を f = (f(0), f(1)) と書く。Aの辺集合 A(1) が直和で A(1) = A(1)1 + A(1)2 と書けるとき、
- f(1)1 := (fの、A(1)1 への制限)
- f(1)2 := (fの、A(1)2 への制限)
として、次の書き方をする。
- f = (f(0), f(1)1 | f(1)2)
この書き方では、「,」より「|」のほうが優先度（結合の強度）が高い。
「,」、「|」では視認性が悪いときは、ALSO, OR を使う。
- f = (f(0) ALSO f(1)1 OR f(1)2)
ラムダ記法
通常のインフォーマルな型付きラムダ記法を用いるが、'λ'の肩に 0, 1 を付けることがある。
- λ0x∈X.( ... ) は、λx∈0X.( ... ) 、あるいは、λx∈X(0).( ... ) と同じ。グラフ射の頂点部分を表す。
- λ1x∈X.( ... ) は、λx∈1X.( ... ) 、あるいは、λx∈X(1).( ... ) と同じ。グラフ射の辺部分を表す。
- 式の値の型は、「∈ B」のような書き方で示すが、このとき「∈1B」や「∈B(1)」とは書かない。頂点・辺の区別（要素の次元）は文脈から読み取る。
- 前節の区切りキーワード ALSO, OR を使って組み合わせる。
同語反復だが、
f:A→B = (
λ0a∈A.(f(0)(a) ∈B)
ALSO
λ1a→a'∈A.(f(1)(a→a') ∈B)
)
または、
f:A→B = (
λ0a∈A.(f(0)(a) ∈B)
ALSO
λ1a→a'∈A.(f(0)(a)→f(0)(a') ∈B)
)
f:A→B, g:C→D に対する f×g の定義：
f×g:A×C→B×D := (
λ0(a, c)∈A×C.( (f(a), g(c)) ∈B×D )
ALSO
λ1(a, c)→(a', c')∈A×C.( (f(a→a'), g(c→c')) ∈B×D )
)
ボックス積
- (A□B)(0) := A(0)×B(0)
- (A□B)(1) := A(1)×B(0) + A(0)×B(1)
s, t の定義は（通常のラムダ記法で示す）：
s:(A□B)(1)→(A□B)(0) := (
λ(a→a', b)∈A(1)×B(0).( (a, b) ∈A(0)×B(0) )
OR
λ(a, b→b')∈A(0)×B(1).( (a, b) ∈A(0)×B(0) )
)
t:(A□B)(1)→(A□B)(0) := (
λ(a→a', b)∈A(1)×B(0).( (a', b) ∈A(0)×B(0) )
OR
λ(a, b→b')∈A(0)×B(1).( (a, b') ∈A(0)×B(0) )
)
1 に関して、1(0) = {0}, 1(1) = {} = 空集合。1□B を計算してみる。
- (1□B)(0) := 1(0)×B(0)
B(0)
- (1□B)(1) := 1(1)×B(0) + 1(0)×B(1) = 1(0)×B(1) B(1)
s, t の定義は（通常のラムダ記法で示す）：
s:(1□B)(1)→(1□B)(0) := (
λ(a, b→b')∈1(0)×B(1).( (0, b) ∈1(0)×B(0) )
)
λb→b'∈B(1).( b ∈B(0) )
t:(1□B)(1)→(1□B)(0) := (
λ(a, b→b')∈1(0)×B(1).( (0, b') ∈1(0)×B(0) )
)
λb→b'∈B(1).( b' ∈B(0) )
以上で、1□B B が示せた。より直接的な λB:1□B→B in SG の表示は（'λ'がかぶっていて、困ったことだが）：
λB:1□B→B := (
λ0(0, b)∈1□B.( b ∈B) /* 頂点部分 */
ALSO
λ1(0, b→b')∈1□B.( b→b' ∈B) /* 辺部分 */
)
この定義に対して、次が可換になるので、λB はグラフ射。
射のボックス積
f:A→B, g:C→D in SG に対して、f□g を定義する。
f□g:A□C→B□D := (
λ0(a, c)∈A□C.( (f(a), g(c)) ∈B□D) /* 頂点部分 */
ALSO
λ1(a→a', c)∈A□C.( (f(a→a'), g(c)) ∈B□D) /* 辺部分 その1 */
OR
λ1(a, c→c')∈A□C.( (f(a), g(c→c')) ∈B□D) /* 辺部分 その2 */
)
実際には、次の可換図式が必要になる。
変形
A, B∈|SG| として、A(0) から B(1) の写像を変形〈deformation〉と呼ぶことにする（一般的な用語ではない）。変形を次の形のラムダ記法で書く。
「...」の部分には、Bの辺を表す式が入る。Aが反射的なとき、頂点にその自己ループ辺を対応させる変形は：
λ01a∈A.( a→a ∈A)
αが A(0)→B(1) の形の変形であることを α:A (0→1) B と書く。ぎごちない記法だが、どうせたいして使わないからいいとする。
α:A (0→1) B に対して、写像 α;s, α;t :A(0)→B(0) が決まる。α;s, α;t は、単なる頂点集合間の写像なので、それがグラフ射を定義するとは限らない。が、もし次の条件が成立しているなら、αをfからgへの変形と呼ぶ。
- α;s = f :A→B かつ α;t = g :A→B
このとき、α:f⇒g と書く。AとBの情報を添えたいときは、α:f⇒g: A (0→1) B と書く（が、面倒だからほとんど書かない）。今後、考える変形は、両端がグラフ射になっているようなものである。
[補足]両端がグラフ射にならない変形の例：
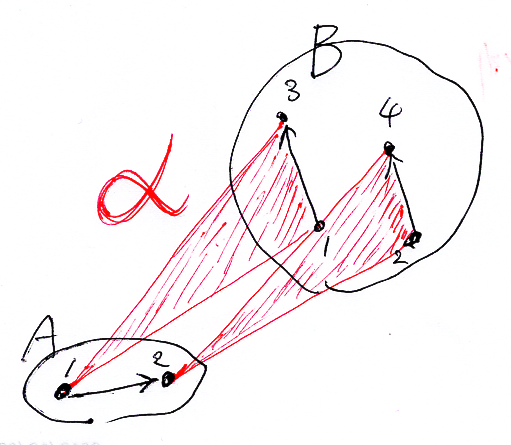
- グラフ A ： A(0) = {1, 2}, A(1) = {1→2}
- グラフ B ： B(0) = {1, 2, 3, 4}, B(1) = {1→3, 2→4}
- 変形 α ： α(1) = 1→3, α(2) = 2→4
変形αの両端を f, g とすると：
- ソース側 ： f(1) = 1, f(2) = 2
- ターゲット側 ： g(1) = 3, g(2) = 4
fもgもグラフ射にはなってない。Aの辺 1→2 の送り先が存在しない。
[/補足]
ホムグラフ
圏はSGしか考えないので、次の略記をする。
- Hom(A, B) = HomSG(A, B) = SG(A, B)
2つの単純グラフ A, B に対して、そのホムグラフ hom(A, B) を次のように定義する。
- |hom(A, B)| = hom(A, B)(0) := Hom(A, B)
- For f, g∈|hom(A, B)|,
hom(A, B)(f, g) := {α | α:f⇒g という変形}
この定義から、ただちに hom(A, B) が単純グラフだと言えるわけではないが、容易に次は分かる。
- A, B∈|SG| ⇒ hom(A, B)∈|SG|
つまり、
- hom(A, B)(f, g) は空集合か単元集合
hom(A, B) は正確に言えば内部ホムグラフで、Hom(A, B) とは次の点で違う。
- Hom(A, B) は外部ホムセット＝普通のホムセットで、単なる集合、グラフ構造は持たない。SGの対象とも考えない。
- hom(A, B) は内部ホム対象で、グラフ構造を持ち、SGの対象と考える。
エバル〈評価射〉
A, B∈|SG| に対して、evA,B:hom(A, B)□A→B を次のように定義する。
evA,B:hom(A, B)□A→B := (
λ0(f, a)∈hom(A, B)□A.( f(a) ∈B)
ALSO
λ1(f⇒f', a)∈hom(A, B)□A.( f(a)→f'(a) ∈B)
OR
λ1(f, a→a')∈hom(A, B)□A.( f(a→a') ∈B)
)
evA,Bは、上記のラムダ記法で定義されるSGの射である。実際には、次の可換図式が必要になる。
カリー化〈随伴転置〉
カリー化〈随伴転置〉は、ホムセット（外部ホムセット）のあいだの写像であり、グラフ射ではない。Hom(A□B, C) の要素 f に対して、A から hom(B, C) へのグラフ射を対応させる。値であるグラフ射の頂点部分は「頂点→グラフ射」で、辺部分は「辺→変形」となる。
ΦA,B,C:Hom(A□B, C)→Hom(A, hom(B, C)) :=
λf∈Hom(A□B, C).(
λ0a∈A.(
(λ0b∈B.( f(a, b) ∈C)
ALSO
λ1b→b'∈B.( f(a, b→b') ∈C)
) ∈hom(B, C)
)
ALSO
λ1a→a'∈A.(
(λ01b∈B.( f(a→a', b) ∈C)) ∈hom(B, C)
)
)
コメント付き：
ΦA,B,C:Hom(A□B, C)→Hom(A, hom(B, C)) :=
λf∈Hom(A□B, C).( /* グラフ射 f:A□B→C が与えられる */
/* ここから下に、
f に対する値である高階グラフ射 F:A→hom(B, C)
を記述する
*/
/* 高階グラフ射 F の頂点部分 */
λ0a∈A.(
/* a∈A(0) に対して、
F(a) はグラフ射 F(a):B→C
*/
(λ0b∈B.( f(a, b) ∈C) /* F(a)(b) := f(a, b) */
ALSO
λ1b→b'∈B.( f(a, b→b') ∈C) /* F(a)(b→b') := f(a, b→b') */
) ∈hom(B, C) /* end of グラフ射 F(a) */
) : A→hom(B, C) /* end of F の頂点部分 */
ALSO
/* 高階グラフ射 F の辺部分 */
λ1a→a'∈A.( /* 辺 a→a' が与えられる */
/* F(a→a') は変形 F(a→a'):B (0→1) C */
( /* 変形は、Bの頂点 b にCの辺を対応させる */
λ01b∈B.(
f(a→a', b) ∈C)
) ∈hom(B, C) /* end of 変形 F(a→a') */
) : A→hom(B, C) /* end of F の辺部分 */
)
