スパイダー〈デルタ〉を持つテンソル計算系では、スパイダー定理が成り立つ。あるいは、スパイダー定理の主張を公理として要請する。
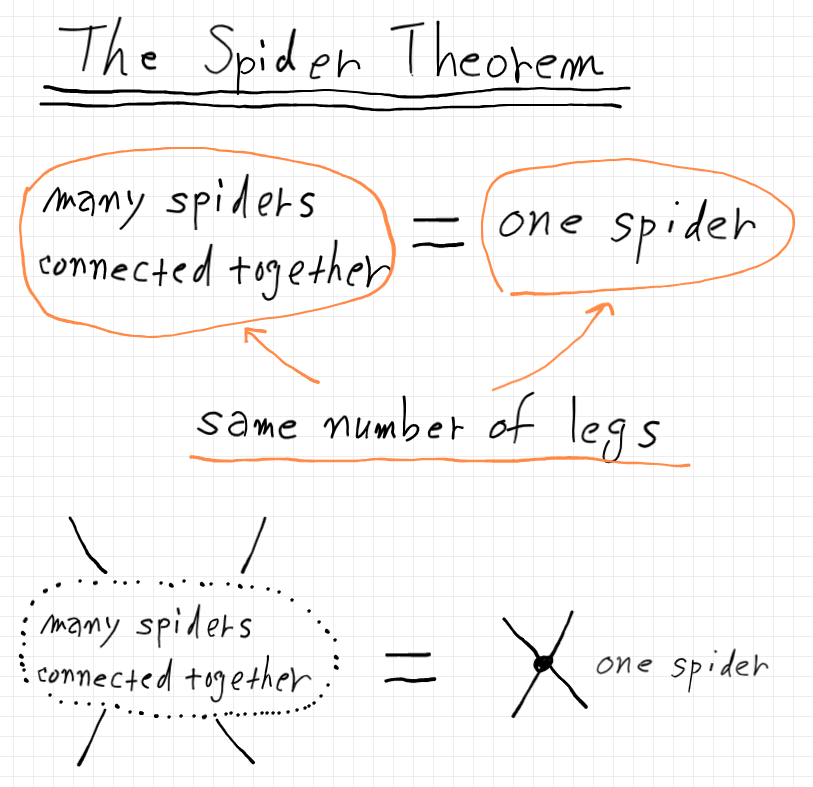
スパイダー定理は包括的な主張だが、より具体的な事例はいくらでも自分で作れるだろう。many spiders が2匹、3匹のときの簡単な事例を4つ。
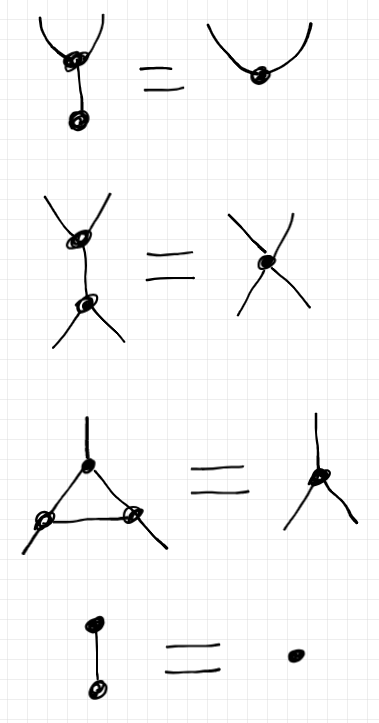
※注: 「2脚スパイダーのドットは描かなくてもよい」というのもスパイダー定理の一部と考えることもあるが、描画のルールと捉えることもできる。実際、三層のケリー/マックレーン・グラフでは2脚でもドットを描く。
スパイダー〈デルタ〉を持つテンソル計算系では、スパイダー定理が成り立つ。あるいは、スパイダー定理の主張を公理として要請する。

スパイダー定理は包括的な主張だが、より具体的な事例はいくらでも自分で作れるだろう。many spiders が2匹、3匹のときの簡単な事例を4つ。

※注: 「2脚スパイダーのドットは描かなくてもよい」というのもスパイダー定理の一部と考えることもあるが、描画のルールと捉えることもできる。実際、三層のケリー/マックレーン・グラフでは2脚でもドットを描く。
内容:
ブール値〈真偽値〉の順序も、普通の記号 $`\le, \lt`$ を使う。$`0 \lt 1`$ のように。ブール値〈真偽値〉の等値も、普通の記号 $`=`$ を使う。$`1 = 1, 0 \ne 1`$ のように。ブール値に対する二項演算 $`(\Imp)`$ の演算結果と順序関係 $`(\le)`$ の真偽が一致するのはたまたまだと割り切って、他の場面まで「$`\Imp`$ と $`\le`$ は同じ」を適用しない!
ブール値関数、つまり述語も普通の関数と同様に扱う。
$`\text{For }X \in |{\bf Set}|\\
\text{For }p, q\in \mrm{Map}(X, {\bf B})\\
\text{Define } p \Imp q := \lambda x\in X.(\, p(x) \Imp q(x) \,)\\
\text{Define } p = q := \forall x\in X. p(x) = q(x)\\
\text{Define } p \le q := \forall x\in X. p(x) \le q(x)\\
\text{Define } p \equiv q := \forall x\in X. p(x) = q(x)
`$
上の定義もオブジェクトレベルの演算や述語をメタレベルで定義していることになるので、[メタ問題]に関わる。メタレベルから見るとき主観位置を変更しているので、[主観位置問題]にも関わる。
次のように書くと、事情が分かりやすくなるかも。$`\mrm{eqBool}`$ はブール値の等値、その他の $`\mrm{xxxBool}`$ も同様。
$`\text{For }X \in |{\bf Set}|\\
\text{We Will Define }\mrm{Imp}_X : \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) \to \mrm{Map}(X, {\bf B}) \In {\bf Set}\\
\text{We Will Define }\mrm{Eq}_X : \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) \to {\bf B}\In {\bf Set}\\
\text{We Will Define }\mrm{Le}_X : \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) \to {\bf B}\In {\bf Set}\\
\:\\
\text{For }p, q\in \mrm{Map}(X, {\bf B})\\
\text{Define } \mrm{Imp}_X(p, q) := \lambda x\in X.(\, \mrm{impBool}(p(x), q(x))\;\in {\bf B} \,)\\
\text{Define } \mrm{Eq}_X(p, q) := \forall x\in X. \mrm{eqBool}(p(x), q(x)) \\
\text{Define } \mrm{Le}_X(p, q) := \forall x\in X. \mrm{leBool}(p(x), q(x))
`$
$`\mrm{Imp}, \mrm{Eq}, \mrm{Le}`$ を対象化して(自分=主観がメタレベルに昇って)プロファイルを書くと:
$`\quad \mrm{Imp} \in \prod_{X\in |{\bf Set}|}\mrm{Map}(\, \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) , \mrm{Map}(X, {\bf B})\,)\\
\quad \mrm{Eq} \in \prod_{X\in |{\bf Set}|}\mrm{Map}(\mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) , {\bf B} )\\
\quad \mrm{Le}\in \prod_{X\in |{\bf Set}|}\mrm{Map}(\mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}) , {\bf B} )
`$
タプルを山形括弧で囲むとして、ラムダ記法だけで定義を書けば:
$`\text{Define }\mrm{Imp} := \\
\quad \lambda\, X\in |{\bf Set}|.\\
\quad \lambda\, \Lis{p, q}\in \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}).(\\
\qquad \lambda\, x\in X.(\, \mrm{impBool}(p(x), q(x))\; \in {\bf B}\,)\; \in \mrm{Map}(X, {\bf B} )\\
\quad )
`$
$`\text{Define }\mrm{Eq} := \\
\quad \lambda\, X\in |{\bf Set}|.\\
\quad \lambda\, \Lis{p, q}\in \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}).(\\
\qquad \forall x\in X.(\, \mrm{eqBool}(p(x), q(x))\,) \in {\bf B}\\
\quad )
`$
$`\text{Define }\mrm{Le} := \\
\quad \lambda\, X\in |{\bf Set}|.\\
\quad \lambda\, \Lis{p, q}\in \mrm{Map}(X, {\bf B})\times \mrm{Map}(X, {\bf B}).(\\
\qquad \forall x\in X.(\, \mrm{leBool}(p(x), q(x))\,) \in {\bf B}\\
\quad )
`$
等値関係が対称であるという事実(正しいと認める命題)をどう書くか?
$`\quad a = b \Iff b = a`$
が普通だろう。次はダメだろうか?
$`\quad (a = b) = (b = a)`$
中央のイコールを関数のイコールと解釈するなら:
$`\text{For }X \in |{\bf Set}|\\
\quad \left(\lambda\, \Lis{a, b}\in X^2.( a = b)\right)
=
\left(\lambda\, \Lis{a, b}\in X^2.( b = a) \right)
`$
関数のイコールはすべての引数値に対して関数値が等しいことだから:
$`\text{For }X \in |{\bf Set}|\\
\quad \forall \Lis{a, b}\in X^2.(\, ( a = b) = ( b = a) \,)
`$
内側のイコールを $`\mrm{eq}`$ と書くと:
$`\text{For }X \in |{\bf Set}|\\
\quad \forall \Lis{a, b}\in X^2. \mrm{eq}(a, b) = \mrm{eq}( b, a)
`$
これは、関数 $`\mrm{eq} : X\times X \to {\bf B}`$ が対称関数であることを主張している。
最初の $`a = b \Iff b = a`$ も同じように、イコールをニ引数関数と解釈すると:
$`\quad \mrm{eq}(a, b) \Iff \mrm{eq}(b, a)`$
$`\Iff`$ は関係記号ではなくて演算子記号だから、次の関数を定義できる。
$`\text{For }X \in |{\bf Set}|\\
\quad \lambda\, \Lis{a, b}\in X^2.(\, \mrm{eq}(a, b) \Iff \mrm{eq}(b, a)\; \in {\bf B}\,)
`$
これは関数を定義しただけなので、「正しい命題だ」という情報がない。それを明示するなら:
$`\text{For }X \in |{\bf Set}|\\
\quad \mrm{True} \le \lambda\, \Lis{a, b}\in X^2.(\, \mrm{eq}(a, b) \Iff \mrm{eq}(b, a)\; \in {\bf B}\,)
`$
ここで、$`\mrm{True}`$ は、$`\mrm{True} \in {\bf B}`$ ではなくて、定数値関数 $`\mrm{True}_X`$ 。
$`\text{For }X \in |{\bf Set}|\\
\text{Define }\mrm{True}_X := \lambda\,x\in X.(\, 1 \;\in {\bf B}\,)
`$
述語 $`p`$ に対して、$`\mrm{True}_X \le p`$ は $`\mrm{True}_X = p`$ と同じ。この事実を書くと:
$`\text{For }X \in |{\bf Set}|\\
\text{For }p \in \mrm{Map}(X, {\bf B})\\
\quad (\mrm{True}_X \le p) \Iff (\mrm{True}_X = p)
`$
話が循環してしまった。
我々(人類)は、名付けと名前解釈の問題で悩み続ける宿命なのだろう。我々は、直示(名付けによらない直接指示)コミュニケーションが特別な(同じ絵を見ていて、指差し可能とかの)場合しか出来ないから、名付け・名指しを避けられない。名指しによらない直示コミュニケーションが出来る宇宙人達は、名前の悩みから開放されているのだろう、羨ましい。
後から思い出したが、伝統的記法でも、“関数そのもの”と“引数を渡した結果である関数値”を区別する書き方はあるにはあった。
伝統的記法と現代的記法の折り合いを付ける手段がラムダ記法で、チャーチ(ラムダ記法の発明者)の功績は計り知れない。
次の状況を考える。
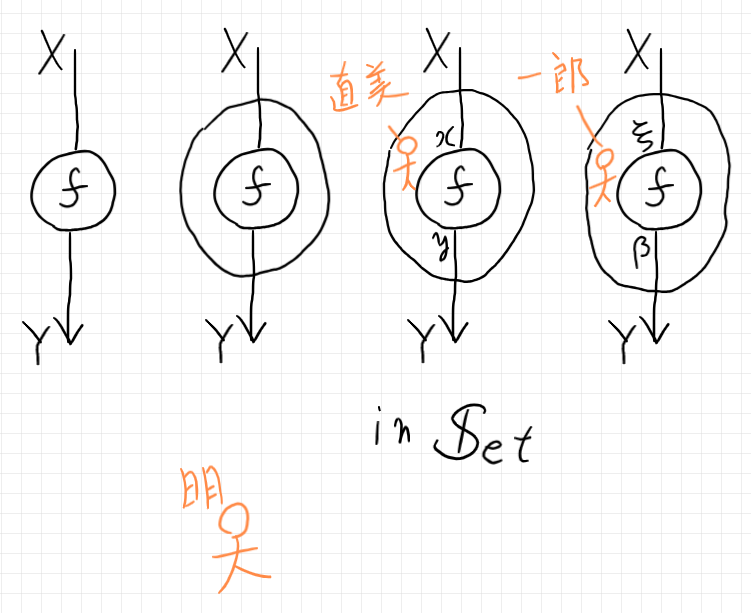
なかのヒトである直美と一郎は、それぞれの趣味により名付けをしている。
彼女・彼のネーミングの情報を伝えるには、伝統的記法が便利。
そとの人である明〈あきら〉は、ポートネーミングに興味がないし、直美や一郎が見えてない。現代的価値観・判断基準を持つ明〈あきら〉から見れば、4つの関数はすべて同じ。このことは次のように表現できる。
$`\quad f = f(\text{-}) = \lambda x. f(x) = \lambda \xi . f(\xi)`$
型もちゃんと書くなら:
$`\quad \lambda x. f(x) = \lambda x\in X.(\, f(x)\; \in Y\,)`$
ラムダ記法により:
今の状況では、明〈あきら〉、直美、一郎は境界線で隔離されている。が、境界線がなくなったり、境界線を越えて名前が漏洩〈リーク〉したりすると、トラブルが起きる。
名前はトラブルのもとであるが、なにかしら名前を付けないとワイヤリングの記述ができない。かくして我々は、名付けと名前解釈の問題で悩み続ける。
「同じだけど違う」「違うけど同じ」に慣れるのは、どうも非常に難しいらしく、慣れるまでに何年もかかるかも知れない。
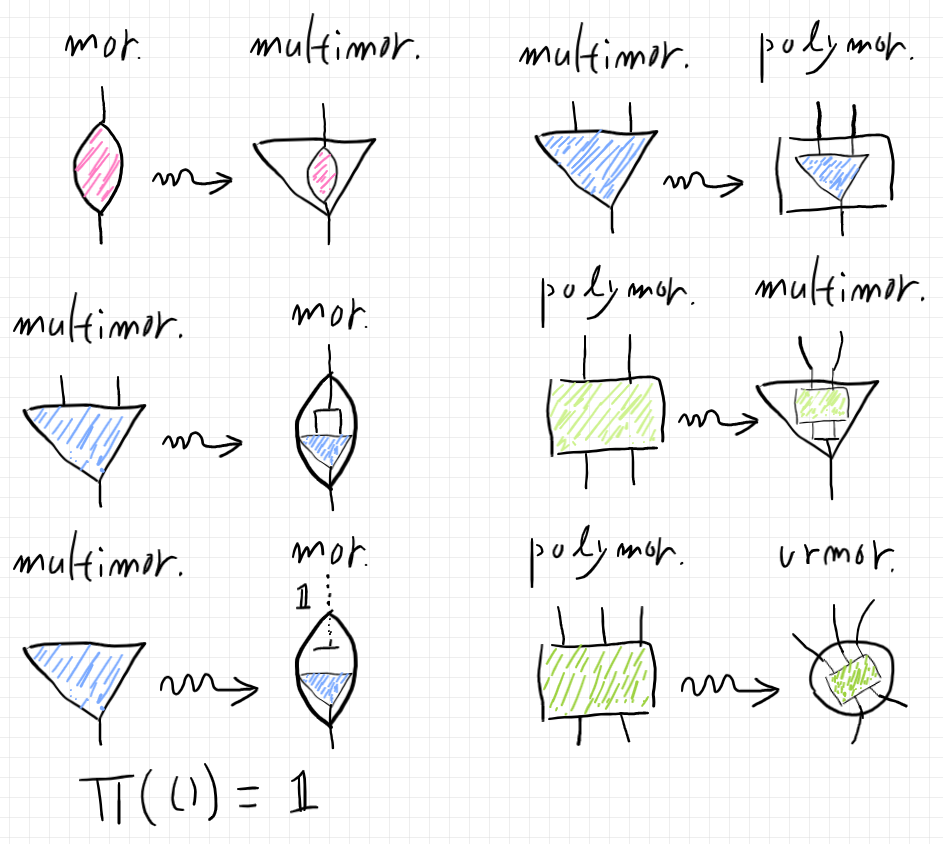
射、複射、多射の三者は相互に変換可能。射 → 複射 → 多射 と規準的〈canonical〉に埋め込める。多射と原射の相互変換は anchor/unanchor〈投錨・抜錨〉 で多様性がある。0本のワイヤーの束を一括〈バンチ〉して1本の $`{\bf 1}`$ ワイヤーが生まれる。その逆もできる。
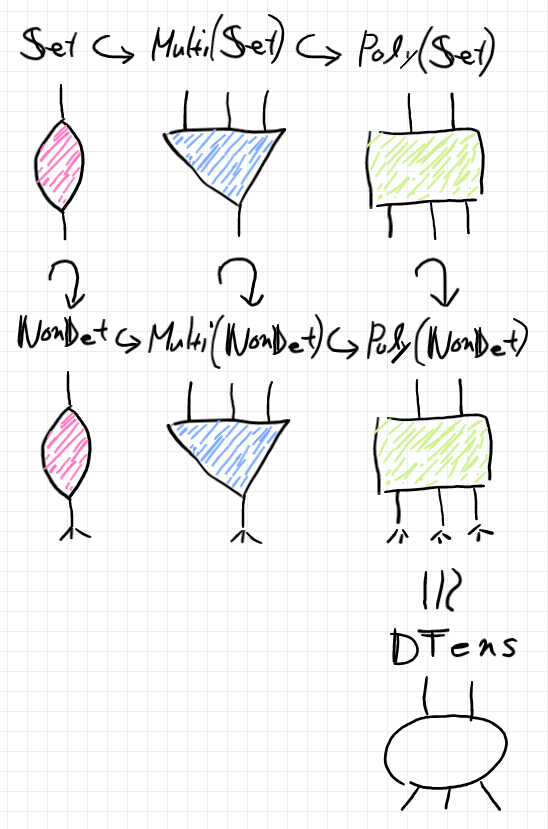
「慣れる」とは、いちいち考えなくても自然に反応できるようになること。サッカーで例えるなら、ボールに慣れるためにリフティング練習やトラップの練習を繰り返す。「慣れる」トレーニングは単純作業的になるのは致し方ない。基礎動作の反復練習とはそういうもの。
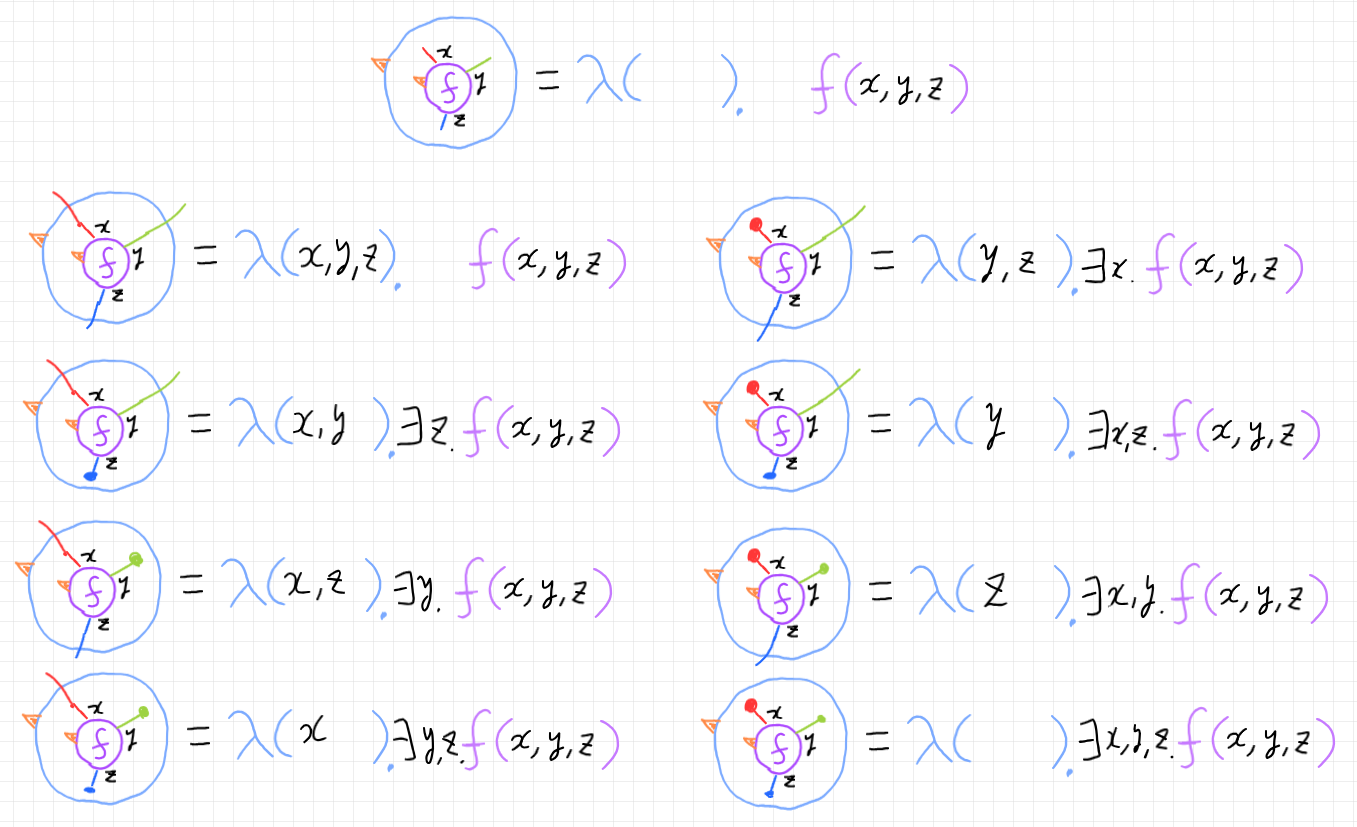
ストリング図の、述語〈ブール値関数〉としてのプロファイル:


色々と紆余曲折・右往左往は忘れて結果だけまとめれば、出現する概念は少数で、後から見れば当たり前だったりする。
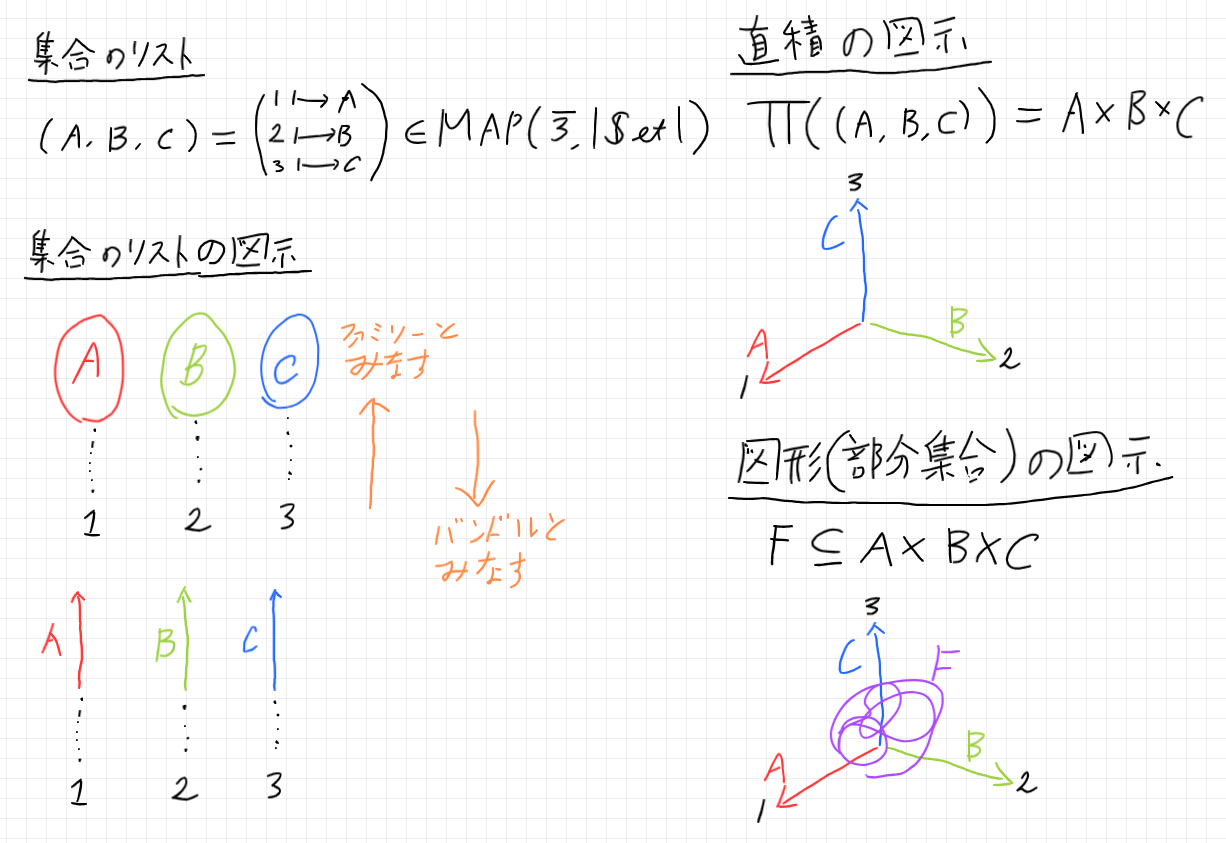
下図の左側は、述語のストリング図表現とラムダ式表現、そのプロファイルをカラフルな絵入りで書いた。
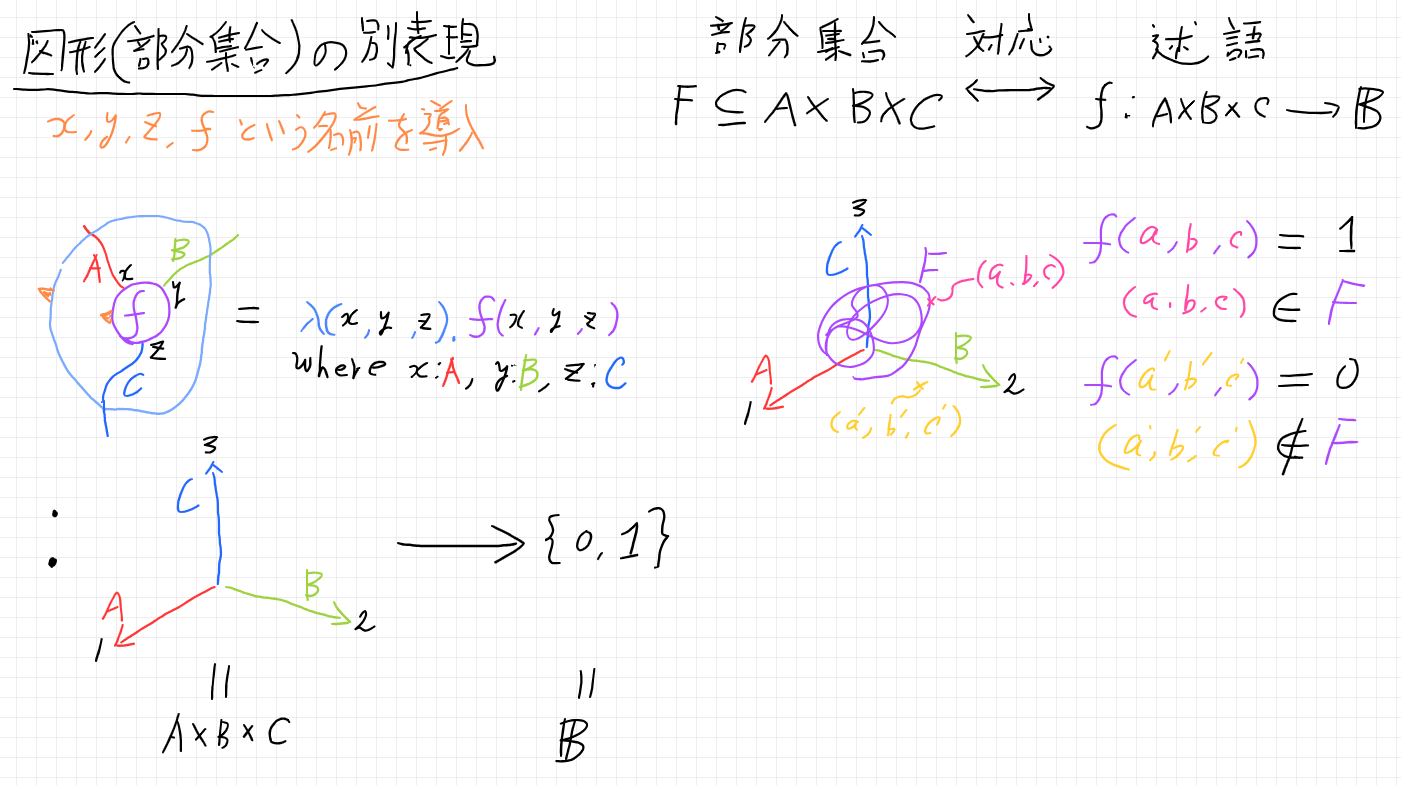
少数の概念を納得したら、あとは分野・コミュニティーごとの異綴同義語の認識。5個の概念に4分野で別々にネーミングすると20個の名前ができる。微妙なズレや変種や冗長表現や分野内方言により、30個、40個、50個(概念の10倍)くらいの呼び名が生じるのは珍しくない。
有限集合に限定すれば、集合 $`A`$ の基数 $`\newcommand{\card}{\mathrm{card} }\card(A)`$ は自然数だとしてよい。
歴史的経緯から、用語はうまく対応しない。今さらどうにもならない。「そう呼ぶのだ」と憶える。
| 数の計算 | 集合の計算 |
|---|---|
| 和 | 直和 |
| 積 | 直積 |
| ベキ〈累乗〉 | 関数空間〈関数集合〉 |
| 総和 | シグマ型 |
| 総積 | パイ型 |
| 2の累乗 | ベキ集合 |
$`\require{color}
%\newcommand{\Imp}{\Rightarrow}
% ---
\newcommand{\In}{ \text{ in }}
%\newcommand{\cat}[1]{\mathcal{#1} }
%\newcommand{\id}{\mathrm{id} }
%\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\mrm}[1]{ \mathrm{#1} }
%\newcommand{\u}[1]{ \underline{#1} }
% ---
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\C}[1]{ \textcolor{blue}{\text{#1}} }
\newcommand{\Definition}{\text{🔴}\Keyword{Definition } }
\newcommand{\WeDefine}{\Keyword{WeDefine } }
\newcommand{\WeWillDefine}{\Keyword{WeWillDefine } }
\newcommand{\WeHaveDefined}{\Keyword{WeHaveDefined } }
%\newcommand{\Notation}{\Keyword{Notation } }
\newcommand{\For}{\Keyword{For } }
\newcommand{\Let}{\Keyword{Let } }
\newcommand{\When}{\Keyword{When } }
\newcommand{\Where}{\Keyword{Where } }
\newcommand{\Then}{\Keyword{Then } }
% ---
\newcommand{\if}{\C{if }}
\newcommand{\then}{\C{ then }}
\newcommand{\else}{\C{ else }}
%`$
$`\Definition\\
\For A \in |{\bf Set}|\\
\WeWillDefine \delta_A : A \to {\bf B} \In {\bf Set}\\
\For a \in A\\
\WeDefine \delta_A(a) := 1 \;\in{\bf B}\\
\Then\\
\WeHaveDefined \delta_A \in {\bf UTens}( (A) )
%`$
$`\Definition\\
\For n \in {\bf N}\\
\WeWillDefine \delta^{(n)} \in
\prod_{S\in \mrm{MAP}(\bar{n}, |{\bf Set}|) } \mrm{Map}(\prod( S), {\bf B})\\
\text{i.e. }\delta^{(n)}_S \in \mrm{Map}(\prod( S), {\bf B})\\
\For S \in \mrm{MAP}(\bar{n}, |{\bf Set}|)\\
\text{i.e. } S \text{ is a table-schema or a profile.}\\
\WeWillDefine \delta^{(n)}_S : \prod( S) \to {\bf B} \In {\bf Set}\\
%
\When n = 0\\
\quad \For S \in \mrm{MAP}(\bar{0}, |{\bf Set}|)\\
\quad \text{i.e. } S = \theta_{|{\bf Set}|} = ()\\
\quad \WeWillDefine \delta^{(0)}_{()} : \prod( () ) \to {\bf B} \In {\bf Set}\\
\quad \WeDefine \delta^{(0)}_{()} := \lambda\, *\in \prod( () ).(\, 1 \;\in {\bf B}\,) \\
\quad \Then\\
\quad \WeHaveDefined \delta^{(0)}_{()} \in {\bf UTens}( () )
\:\:\Where ()\in \mrm{MAP}(\bar{0}, |{\bf Set}|)\\
%
\When n = 1\\
\quad \For S \in \mrm{MAP}(\bar{1}, |{\bf Set}|)\\
\quad \text{i.e. } S = (A) \text{ for some }A\in |{\bf Set}|\\
\quad \Let A := S(1) \; \in|{\bf Set}|\\
\quad \Then S = (A)\\
\quad \WeWillDefine \delta^{(1)}_{(A)} : \prod( (A) ) \to {\bf B} \In {\bf Set}\\
\quad \WeDefine \delta^{(1)}_{(A)} := \lambda\, a\in \prod( (A) ).(\, 1 \;\in {\bf B}\,) \\
\quad \Then\\
\quad \WeHaveDefined \delta^{(1)}_{(A)} \in {\bf UTens}( (A) )
\:\:\Where (A)\in \mrm{MAP}(\bar{1}, |{\bf Set}|)\\\\
%
\When n = 2\\
\quad \For S \in \mrm{MAP}(\bar{2}, |{\bf Set}|)\\
\quad \text{i.e. } S = (A, B) \text{ for some }A, B \in |{\bf Set}|\\
\quad \Let A := S(1), B = S(2) \; \in|{\bf Set}|\\
\quad \Then S = (A, B)\\
\quad \WeWillDefine \delta^{(2)}_{(A, B)} : \prod( (A, B) ) \to {\bf B} \In {\bf Set}\\
\quad \WeDefine \delta^{(2)}_{(A, B)} := \lambda\, (a, b)\in \prod( (A, B) ).(\\
\qquad (\if a = b \then 1 \else 0) \;\in {\bf B}\,) \\
\quad \Then\\
\quad \WeHaveDefined \delta^{(2)}_{(A, B)} \in {\bf UTens}( (A, B) )
\:\:\Where (A, B)\in \mrm{MAP}(\bar{2}, |{\bf Set}|)\\\\
%
\When n \ge 3\\
\quad \For S \in \mrm{MAP}(\bar{n}, |{\bf Set}|)\\
\quad \WeWillDefine \delta^{(n)}_{(S(1), \cdots, S(n)) } : \prod( (S(1), \cdots, S(n) ) ) \to {\bf B} \In {\bf Set}\\
\quad \WeDefine \delta^{(n)}_{(S(1), \cdots, S(n))} := \lambda\, (a_1,\cdots, a_n)\in \prod( (S(1), \cdots, S(n)) ).(\\
\qquad \prod_{i, j\in \bar{n}} \delta^{(2)}_{( S(i), S(j) )}(a_i, a_j) \;\in {\bf B}\,) \\
\quad \Then\\
\quad \WeHaveDefined \delta^{(n)}_{S} \in {\bf UTens}( S )
\:\:\Where S \in \mrm{MAP}(\bar{n}, |{\bf Set}|)\\
\Then\\
\WeHaveDefined \delta \in \prod_{n\in {\bf N}}\prod_{S\in \mrm{MAP}(\bar{n}, |{\bf Set}|) } {\bf UTens}( S)
%`$
「絵の描き方 3: 行列の掛け算」の続き、テンソルは主にブーリアン係数。
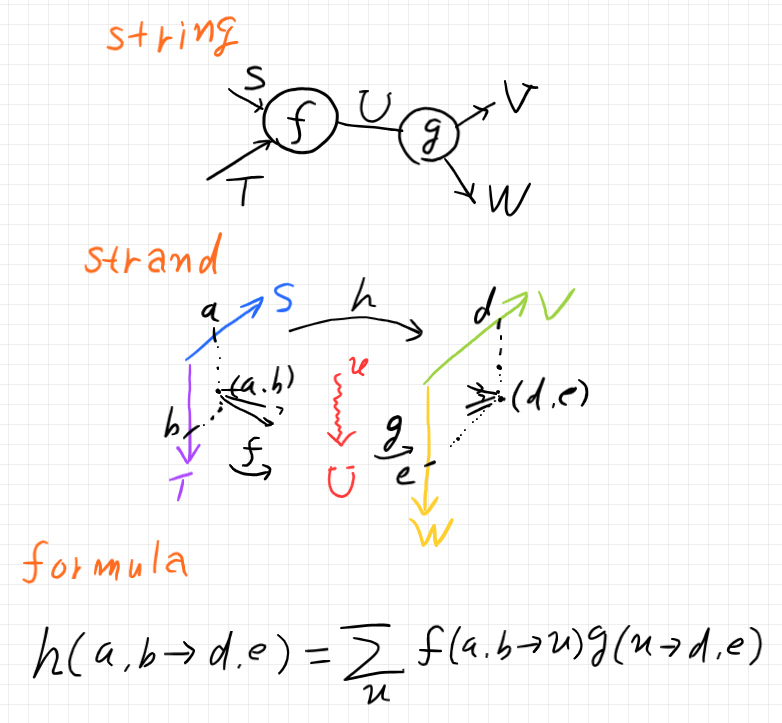
ストリング図:
ストランド図:
数式:
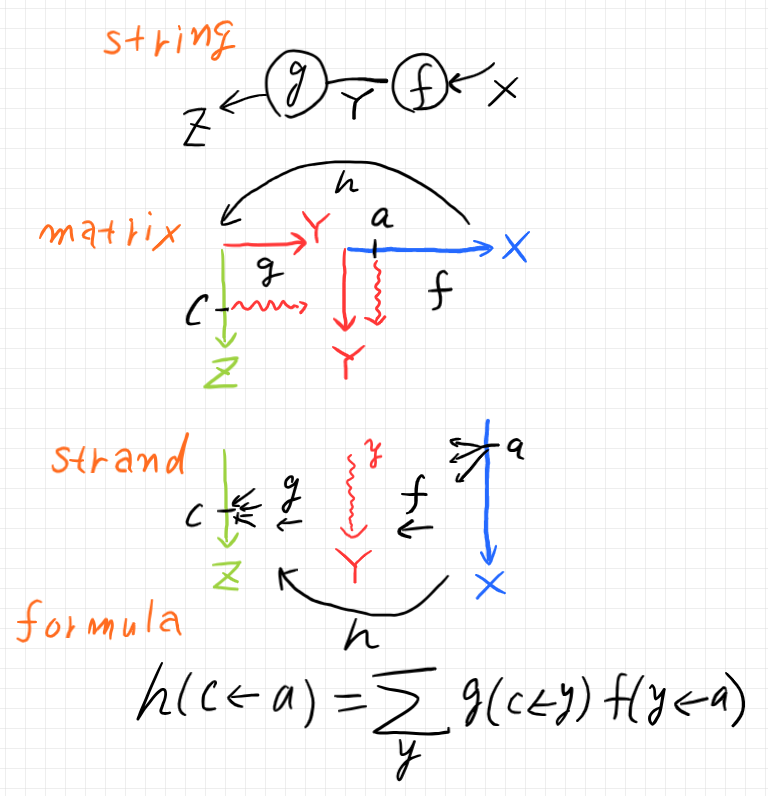
ストリング図:
行列の掛け算:
ストランド図:
数式: