集合圏における可換図式による法則の記述 (C A3P2) - (2nd) 檜山正幸のキマイラ飼育記

問題文はピンク文字で書いてある。
「p.3」などのページ参照は、第2回メイン資料（紙）のページ番号。

後から次の追記・修正を行った。

第2回メイン資料（紙）への参照を追加。
ラムダ記法の解説を追加。
集合圏の重要な射の定義を追加。
マックレーンの五角形／三角形の例を追加。
その他些細な修正。

※ 練習問題の解答は「解答：集合圏における可換図式による法則の記述 (C A6R2)」にあります。

内容：

事前の了解事項
ラムダ記法
集合圏の重要な対象と射
- 集合圏の重要な対象
- 集合圏の重要な射
可換図式による法則の記述

事前の了解事項

$\require{AMScd} \newcommand{\id}{\mbox{id}} \newcommand{\zero}{{\bf 0}} \newcommand{\one}{{\bf 1}} \newcommand{\two}{{\bf 2}} \newcommand{\F}{\mbox{F}} \newcommand{\T}{\mbox{T}} \newcommand{\true}{\mbox{true}} \newcommand{\false}{\mbox{false}} \newcommand{\eq}{\mbox{eq}}$ だいたい口頭で説明しているが：

アンダースコアを無名ラムダ変数とする簡易ラムダ式を使う。例： (_+_) は足し算の関数、(-_) は単項マイナス（符号反転）の関数。次節に解説を追加。p.5 - p.6「集合圏」も参照。
要素の代わりに出来るだけポイント{射}?〈{pointing | point} {morphism}?〉 p:1→A を使う。p.6参照。
写像〈関数〉の直積は、(f×g)(x, y) := (f(x), f(y)) で定義される。p.6参照。
述語{関数}? p, q に対する p = q は、述語{関数}?を命題とみなせば p ⇔ q 。
述語{関数}? p:A→2 に対する p = T_A は、「p が成立する」と同じ。T_A の定義は後述。
図式（全体）が可換だとは、図式内の任意の2点を結ぶパスが（射として）等しいこと。p.5「図式と可換図式」を参照。

ラムダ記法

ラムダ計算の知識が必要なわけではなく、インフォーマルな（多少イイカゲンな）ラムダ記法を知っていれば十分。

ラムダ記法とは、関数を表す書き方で、次のように書く。

λ変数名∈域の集合.(式 ∈余域の集合)

例えば、二次関数（で一番簡単なヤツ）なら、

λx∈R.(x² ∈R)

ここでの（実は世間でも一般的な）約束として、二変数関数とペアの一変数関数を区別しない。つまり、

f(x, y) = f((x, y))

ちゃんと考えると、この等式は明らかに間違ってる。ちゃんとした等式として捉えるのではなくて、コミュニケーション上のお願いが書いてあると解釈する。記号の乱用〈abuse of notation〉（p.3参照）ですな。

二変数に限らず多変数関数とタプルの一変数関数を、記号の乱用により区別しない。必要があれば、各自区別して厳密に考えてくださいな。口頭であれだけクドく言ったように、数学のコミュニケーションとは、こういうイイカゲンさに満ち溢れている。別なセミナー（ゲーデルの不完全性定理二期）用の記事だが「現実世界の不整合や不合理は受け入れよう」も参照。用語・記法の混乱は破綻寸前だが、どうにもならんものはどうにもならん*1。

話を戻して、自然数の足し算の関数はラムダ記法で次のように書ける。

λ(x, y)∈N×N.(x + y ∈N)

この関数に、nat_add と名前を付けるなら、

nat_add := λ(x, y)∈N×N.(x + y ∈N)

関数〈写像〉 nat_add のプロファイル（域と余域の情報）は、nat_add:N×N→N。

変数が自然数を表すと前提されていれば、ラムダ記法のなかに域、余域を書かなくてもいい。

nat_add := λ(x, y).(x + y)

ラムダ変数（記号'λ'の直後に現れる入力を表す変数）をアンダースコアで書くと約束すると（名前がなくなるので、2つの変数の区別は出来なくなる）：

nat_add := (_ + _)

これだったら、nat_add と名前で書くより、直接 (_ + _) でいいじゃん -- となり、演算子記号を関数記号扱いするときは、(_+_), (_×_), (-_), (_!), (_)² などが使われる。「!」は階乗〈factorial〉関数を表す後置演算子記号である。

問題 1：

次の値を求めよ。

(_+_)(2, 3)
(_+_)((_×_)(2, 3), (_×_)(4, 5))
(_+_)((_×_)(2, (_)²(3)), (_×_)(2, 3))
(_+_)(3, (_+_)(1, 7))
(_+_)((_+_)(3, 1), 7)
(_x_)((_!)(3), (_+_)(1, 1))

二項演算子に関しては、アンダースコアも省略していいとする。その書き方だと：

(+)(2, 3)
(+)((×)(2, 3), (×)(4, 5))
(+)((×)(2, (_)²(3)), (×)(2, 3))
(+)(3, (+)(1, 7))
(+)((+)(3, 1), 7)
(x)((_!)(3), (+)(1, 1))

注意：

無名ラムダ変数には、ハイフン（マイナス記号）が最もよく使われる。檜山がアンダースコアにしたのは、(_-_), (-_) がハイフンだとうまく書けないから。しかし、アンダースコアは名前の一部に使われる（かも知れない）、という問題もある。' $\ast$ ', ' $\cdot$ ' を無名ラムダ変数に使う人もいる -- 演算子記号と混同する危険がある。記号・記法は、どう選んでもなにかしらの問題はあるもんだ。
(+) などはHaskellの記法と同じだが、カリー化はしてないので、(+) 2 3 ではなくて (+)(2, 3) と書く。

問題 2：

2 = {0, 1} として、関数 (∧), (∨):2×2→2, (￢_):2→2 を次のように定義する。

1∧1 = 1, 0∧1 = 0, 1∧0 = 0, 0∧0 = 0
1∨1 = 1, 0∨1 = 1, 1∨0 = 1, 0∨0 = 0
￢1 = 0, ￢0 = 1

次の値を求めよ。

(∨)((∧)(1, 1), (∧)(1, 0))
(￢_)((∧)(1, 1))
(￢_)((￢_)((∨)(1, 0)))
(∨)((￢_)((∧)(1, 0)), (￢_)((∧)(0, 1)))

問題 3：

(=), (≦):N×N→2 は、普通の（小学校以来お馴染みの）等号と不等号を表す関数だとする。

次の値を求めよ。

(=)((+)(1, 1), 2)
(∨)((≦)(1, 2), (=)(1, 2))
(∧)((≦)(1, 2), (=)(1, 2))
(∧)((≦)(1, 2), (￢_)((=)(1, 2)))
(∧)((≦)(1, 2), (≦)(2, 1))
(￢_)((∧)((≦)(2, 2), (≦)(2, 2)))

ラムダ記法／ラムダ計算をもっと知りたいなら、次の記事が入門になるだろう。

微分計算や微分幾何でもラムダ記法は使ったほうがいい、という話は：

集合圏の重要な対象と射

集合圏の重要な対象

空集合： ${\bf 0}$
特定された単元集合： ${\bf 1}$ （唯一の要素はなんでもいいが、{0} としておく。）
特定された二元集合： ${\bf 2}$ （二つの要素はなんでもいいが、{0, 1} としておく。）

集合圏の重要な射

記号	名称	英語
$\alpha$	結合律子	associator
$\lambda$	左単位律子	left unitor
$\rho$	右単位律子	right unitor
$!$	-	discharger, discarder
$\Delta$	複製子	duplicator, copier
$\pi_1$	第一射影	first projection
$\pi_2$	第ニ射影	second projection
$\sigma$	対称、互換	symmetry, transposition
$\theta$	-	-
$\T$	真	true
$\F$	偽	false
$\eq$	等値	equal

記号	添字付き	プログラム風	意味的名前
$\alpha$	$\alpha_{A,B,C}:(A\times B)\times C\to A\times (B\times C)$	alpha<A, B, C>	assoc<A, B, C>
$\lambda$	$\lambda_A:\one\times A \to A$	lambda<A>	lunit<A>
$\rho$	$\rho_A:A\times\one \to A$	rho<A>	runit<A>
$!$	$!_A:A\to \one$	bang<A>	void<A>
$\Delta$	$\Delta_A:A\to A\times A$	Delta<A>	dup<A>
$\pi_1$	${\pi_1}_{A,B}:A\times B \to A$	pi[1]<A, B>	proj[1]<A, B>
$\pi_2$	${\pi_2}_{A,B}:A\times B \to B$	pi[2]<A, B>	proj[2]<A, B>
$\sigma$	$\sigma_{A,B}:A\times B \to B\times A$	sigma<A, B>	transpos<A, B>
$\theta$	$\theta_A:\zero\to A$	theta<A>	empty<A>
$\T$	$\T_A:A\to \two \:\:(\T_A := \;!_A;\true )$	T<A>	True<A>
$\F$	$\F_A:A \to \two \:\:(\F_A := \;!_A;\false)$	F<A>	False<A>
$\eq$	$\eq_A:A\times A \to \two$	eq<A>	eq<A>

表〈ひょう〉に現れた関数〈写像〉の定義を以下に示す。ラムダ記法の'λ'と左単位律子の'λ'がカブる（コンフリクトする）ので、ラムダ記法の'λ'に上線を付ける。 $\newcommand{\fun}{ \overline{ \lambda} \;}$

$\alpha_{A,B,C} := \fun ( (a, b), c) \in (A\times B)\times C.(\, ( a, (b, c)) \:\in A\times (B\times C) \,)$
$\lambda_A := \fun (0, a)\in \one\times A .(\, a \:\in A \,)$
$\rho_A := \fun (a, 0) \in A\times \one .(\, a \:\in A \,)$
$!_A := \fun a \in A .(\, 0 \:\in \one \,)$
$\Delta_A := \fun a \in A .(\, (a, a) \:\in A\times A \,)$
${\pi_1}_{A,B} := \fun (a, b) \in A\times A .(\, a \:\in A \,)$
${\pi_2}_{A,B} := \fun (a, b) \in A .(\, b \:\in B \,)$
$\sigma_{A, B} := \fun (a, b) \in A\times B .(\, (b, a) \:\in B\times A \,)$
$\theta_A$ ラムダ記法では表現不可能。空集合0から任意の集合Aへの写像はただひとつある、それを $\theta_A$ とする。
$\true := \fun x \in \one .(\, 1 \:\in \two \,)$
$\false := \fun x \in \one .(\, 0 \:\in \two \,)$
$\T_A := \fun a \in A .(\, 1 \:\in \two \,)$
$\F_A := \fun a \in A .(\, 0 \:\in \two \,)$
$\eq_A := \fun (a, b) \in A\times A .(\, (a = b) \:\in \two \,)$

注意：

α, λ, ρ, σ は可逆（同型射）なので、常に逆射が存在する*2。例： ${\lambda_A}^{-1}:A \to \one\times A$
πの添字 1, 2 は上にすることも多い*3、π¹, π²。
$\true, \false:\one \to \two$ は、二元集合の異なる要素をポインティングする写像。
表のなかで、θより下は記法が安定してない。同義な記号が幾つかある。
1. θと同義： ¡_A, $\emptyset_A$ （¡ は逆感嘆符）
2. Tと同義： $\mbox{True}_A,\; \true_A,\; \mbox{t}_A$
3. Fと同義： $\bot_A,\; \mbox{False}_A,\; \false_A$
4. eqと同義： $=_A,\; \mbox{Eq}_A$

可換図式による法則の記述

注意：

「ナントカ{の}?法則」と「ナントカ律」は同じ。
ここでの「演算」は「二項演算」
ここでの「関係」は「二項関係」、対応する述語関数（2を余域とする関数）で関係を表現する。
"composition"も"associative"も「結合」なので注意（オーバーロード）。
可換律の「可換」は、二項演算の引数順序を交換できること。可換図式の「可換」は、図式内の二点を結ぶパスが（射として）等しいこと。「可換」がオーバーロードされているので、意味は文脈で判断。

約束：

e, m, S, r は次のようなプロファイル（域と余域）を持つ射（集合圏では写像〈関数〉）だとする。

e:1→A （eはポイント射）
m:A×A→A （mは二項演算）
S:A→A （Sは単項演算）
r:A×A→2 （rは二項述語関数）

問題 4：

最初は、可換図式を見ても「なんじゃこりゃ?!」としか思えないだろう。そこで、次の作業をしてみよう。

可換図式と同じレイアウトで、集合の要素を追いかける図を描く。
集合の要素を追いかける図から、等式を書いてみる。
書き下した等式と、もとの可換図式が意味的には同じことを納得する。

例題として、次の3つの法則には、集合の要素を追いかける図と等式を添える。

演算 m の結合律
演算 m の可換律
関係 r の反対称律

他の法則については各自やってみよ（練習問題）。

演算 m の結合律

$\begin{CD} A\times A\times A @>m\times \mbox{id}_A>> A\times A \\ @V \mbox{id}_A\times m VV @VV m V \\ A\times A @>m>> A \end{CD}$

集合の要素を追いかける図

$\begin{CD} (a, b, c) @>m\times \mbox{id}_A>> (m(a, b), c) \\ @V \mbox{id}_A\times m VV @VV m V \\ (a, m(b, c)) @>m>> 下右 \;m(a,m(b,c)), 右下 \;m(m(a, b), c) \end{CD}$

等式

右下 = 下右
$m(m(a, b), c) = m(a,m(b,c))$

注意：

可換図式を簡略化している（αを書いてない）ので、要素の追いかけで少しインチキをしている。正確にやりたいのなら、次にある図式を使う。次の図式には、((a, b), c) と (a, (b, c)) の変換であるαもちゃんと入っている。

演算 m の結合律（もっと正確に）

$\begin{CD} (A\times A)\times A @>m\times \mbox{id}_A>> A\times A \\ @V\alpha_{A,A,A}VV @| \\ A\times (A\times A) @. {} \\ @V \mbox{id}_A\times m VV @VV m V \\ A\times A @>m>> A \end{CD}$

注意：

A×A が抜けているが（空白）、これは容易に補完できるから。以下で、容易に補完できるところは空白になっていることがある。

演算 m の左単位律

$\begin{CD} A @>{{\lambda_A}^{-1}}>> \one\times A \\ @| @VV{e\times \mbox{id}_A}V \\ A @<{m}<< A\times A \end{CD}$

演算 m の右単位律

$\begin{CD} A @>{{\rho_A}^{-1}}>> A\times\one \\ @| @VV{\mbox{id}_A\times e}V \\ A @<{m}<< A\times A \end{CD}$

演算 m の可換律

$\begin{CD} A\times A @>{\sigma_{A,A}}>> A\times A \\ @V{m}VV @VV{m}V \\ A @= A \end{CD}$

集合の要素を追いかける図

$\begin{CD} (a, b) @>{\sigma_{A,A}}>> (b, a) \\ @V{m}VV @VV{m}V \\ m(a, b) @= 下右 \; m(a, b), 右下 \; m(b, a) \end{CD}$

等式

下右 = 右下
m(a, b) = m(b, a)

演算 m のベキ等律

$\begin{CD} A @>{\Delta_A}>> A\times A \\ @| @VV{m}V \\ {} @= A \end{CD}$

演算 m の左逆元

$\begin{CD} A @>{\Delta_A}>> A\times A \\ @V{!_A;e}VV @VV{S \times \mbox{id}_A}V \\ A @<{m}<< A\times A \end{CD}$

演算 m の右逆元

$\begin{CD} A @>{\Delta_A}>> A\times A \\ @V{!_A;e}VV @VV{\mbox{id}_A \times S}V \\ A @<{m}<< A\times A \end{CD}$

関係 r の反射律

$\begin{CD} A @>{\Delta_A}>> A\times A \\ @| @VV{r}V \\ {} @>{\T_A}>> \two \end{CD}$

関係 r の対称律

$\begin{CD} A\times A @>{\sigma_{A,A}}>> A\times A \\ @V{r}VV @VV{r}V \\ \two @= \two \end{CD}$

関係 r の反対称律

$\begin{CD} A\times A @>{\Delta_{A\times A}}>> (A\times A)\times(A\times A) \\ @V{\eq_A}VV @VV{r\times (\sigma_{A,A} \;;\; r)}V \\ \two @<{(\_\land\_)}<< \two\times\two \end{CD}$

集合の要素を追いかける図

$\begin{CD} (a, b) @>{\Delta_{A\times A}}>> ( (a, b), (a, b) ) \\ @V{\eq_A}VV @VV{r\times (\sigma_{A,A}\;;\; r)}V \\ 下 \; \eq(a, b), 右下左 \; r(a, b)\land r(b, a) @<{(\_\land\_)}<< (r(a, b), r(b, a)) \end{CD}$

等式

右下左 = 下
真偽値が等しいことは命題が同値なことだから、
右下左 ⇔ 下
$r(a, b)\land r(b, a) \Leftrightarrow \eq(a, b)$

関係 r の推移律

推移律を可換図式で表すことに実用的意義味があるかどうかは疑わしい。論理の予備知識がけっこう要るし、複雑になるので嬉しくないが、練習問題として考えるのはまーいいだろう。分からなくても気にする必要はない。

まず、関数 (_⇒_):2×2→2 を次のように定義する。

1⇒1 = 1, 0⇒1 = 1, 1⇒0 = 0, 0⇒0 = 1

LとRは後で定義するとして：

$\begin{CD} (A\times A)\times A @>{\Delta_{(A\times A)\times A}}>> ( (A\times A)\times A)\times ( (A\times A)\times A) \\ @V{\T_{(A\times A)\times A}}VV @V{L \times R}VV \\ \two @<{(\_\Rightarrow\_)}<< \two \times \two \end{CD}$

Lの定義：

次の図式が可換になるように、L を定義する。

$\begin{CD} (A\times A)\times A @>{\Delta_{(A\times A)\times A}}>> ( (A\times A)\times A)\times( (A\times A)\times A) \\ @| @VV{ {\id_{(A\times A)\times A}} \:\: \times\, \alpha_{A,A,A}}V \\ {} @. ( (A\times A)\times A)\times(A\times (A \times A)) \\ @| @VV{(r\times !_A) \times (!_A\times r)}V \\ {} @. (\two\times\one)\times(\one\times\two) \\ @V{L}VV @VV{\rho_{\two} \,\times\, \lambda_{\two}}V \\ \two @<{(\_\land\_)}<< \two\times\two \end{CD}$

次の等式でも同じ。
$L :=\; \Delta_{(A\times A)\times A} \,;\, \id_{(A\times A)\times A}\times \alpha_{A,A,A} \,;\, (r\times !_A) \times (!_A\times r) \,;\, \rho_{\two}\times \lambda_{\two} \,;\, (\_\land\_)$

Rの定義：

次の図式が可換になるように、R を定義する。

$\begin{CD} (A\times A)\times A @>{\alpha_{A,A,A}}>> A\times(A\times A) \\ @| @VV{\id_A \,\times\, \sigma_{A,A}}V \\ {} @. A\times(A\times A) \\ @| @VV{{\alpha_{A,A,A}}^{-1}}V \\ {} @. (A\times A)\times A \\ @V{R}VV @VV{{\pi_1}_{A\times A, A}}V \\ \two @<{r}<< A\times A \end{CD}$

次の等式でも同じ。
$R :=\; \alpha_{A,A,A} \,;\, \id_A \times \sigma_{A,A} \,;\, {\alpha_{A,A,A}}^{-1} \,;\, {\pi_1}_{A\times A, A} \,;\, r$

推移律を可換図式で表現した（論理式を逐語訳した）ときの煩雑さにウンザリしたかも知れないが、定義や定式化はひととおりではない。同じ概念を定義／定式化する様々な方法があるから、目的に応じてふさわしい方法を選べばよい。例えば、関係を関係圏Relの射 r として定義すれば、r の推移性は次のように極めて短く記述できる。

r:A→A in Rel が推移的 ⇔ r;r ⊆ r

特定の定義／定式化に固執したり絶対視してはいけない。

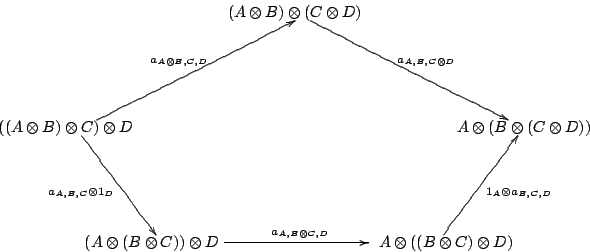
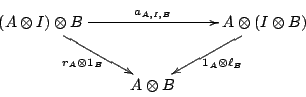
マックレーンの五角形、三角形

次の2つの図式が、集合圏において可換になることを確認せよ。

$\begin{CD} ( (A\times B)\times C)\times D @>\alpha_{A\times B,C,D}>> (A\times B) \times (C\times D) \\ @| @VV \alpha_{A,B,C\times D} V \\ {} @. A\times (B \times (C\times D) ) \\ @V \alpha_{A,B,C}\;\times \mbox{id}_D VV @AA {\mbox{id}_A\times \alpha_{B,C,D}} A \\ (A \times (B \times C))\times D @>\alpha_{A,B\times C,D}>> A\times ( (B\times C)\times D) \end{CD}$

$\begin{CD} (A\times \one) \times B @>\alpha_{A,\one, B}>> A\times (\one\times B) \\ @V{\rho_A\times \id_B}VV @V{\id_A \times \lambda_B}VV \\ A\times B @= A\times B \end{CD}$

この2つの可換図式は、マックレーンの五角形、マックレーンの三角形と呼ばれるが、その内容（モノイド圏の一貫性）はちょっと難しいので割愛。2つの図式が実際に五角形／三角形になってないのは、四角形にしかレイアウトできないLaTeX（実際はMathJax）パッケージを使っているから（「MathJaxで可換図式」参照）。下図（これは画像）のレイアウトは五角形／三角形。

*1:ほんとに破綻して、にっちもさっちもいかなくなったら、改善・改良されるだろう。それまでは、マズイと分かっていても習慣と惰性が強すぎて直る見込みがない。

*2:f:A→B と g:B→A が互いに逆だとは、f;g = id_A かつ g;f = id_B であること。gはfの逆射で、fはgの逆射という。

*3:上付き添字は累乗だと思い込んでいる人が多いだろう。上付き添字は累乗以外の様々な目的で使われる。「x²」が「xの二乗」とは限らない。次の記事を読んで、記号の使い方と意味を固定化しないようにしよう。