ちょっとずつ追加・修正の予定。概念の解説はここではしない。描画法のみ列挙する。
基本
上下左右が入り乱れること:
ストリング図に関する比較的詳しい説明:
後で出てくるタイプ・アノテーション〈プロファイル・アノテーション〉をルビ風に付ける方法は:
以下に出てくる絵で、☆は単一対象と恒等射だけからなる自明圏。f::A⇒B:☆→C in CAT と f:A→B in C は適宜相互に置き換えて解釈する(これがコツ)。この手法については:
関手の関手性
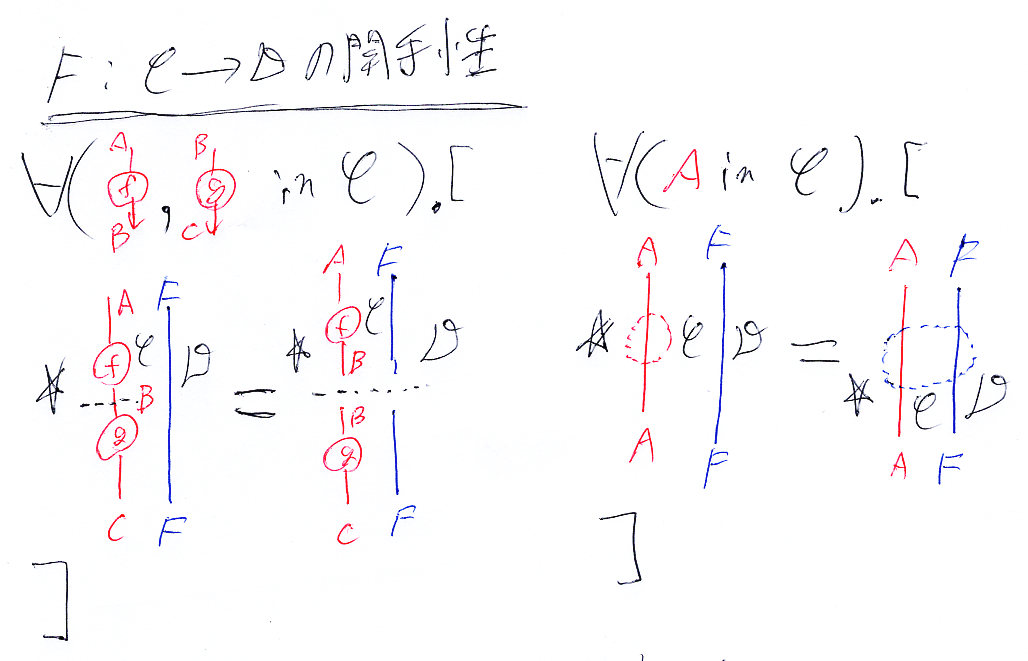
図式順記法で、絵を書き写す。一時的に、関手の矢印は波矢印を使う(谷村省吾先生流)。
結合に関して:
恒等射に関して:
アノテーションが鬱陶しいので除くと:
反図式順記法で:
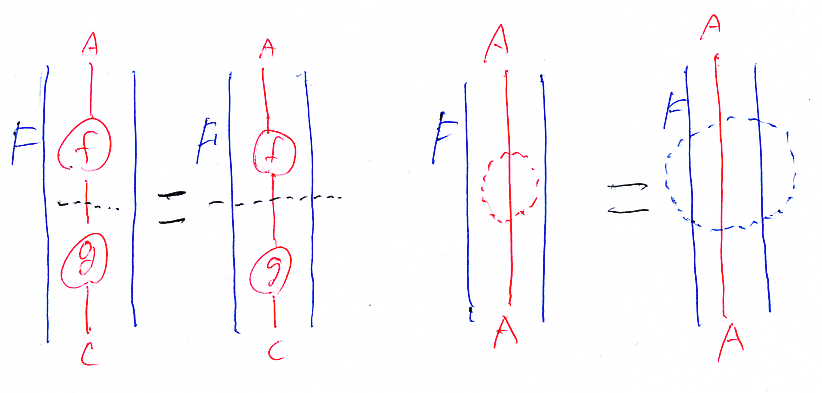
ちなみに、同じことをストライプ図で描くと:
自然変換の自然性
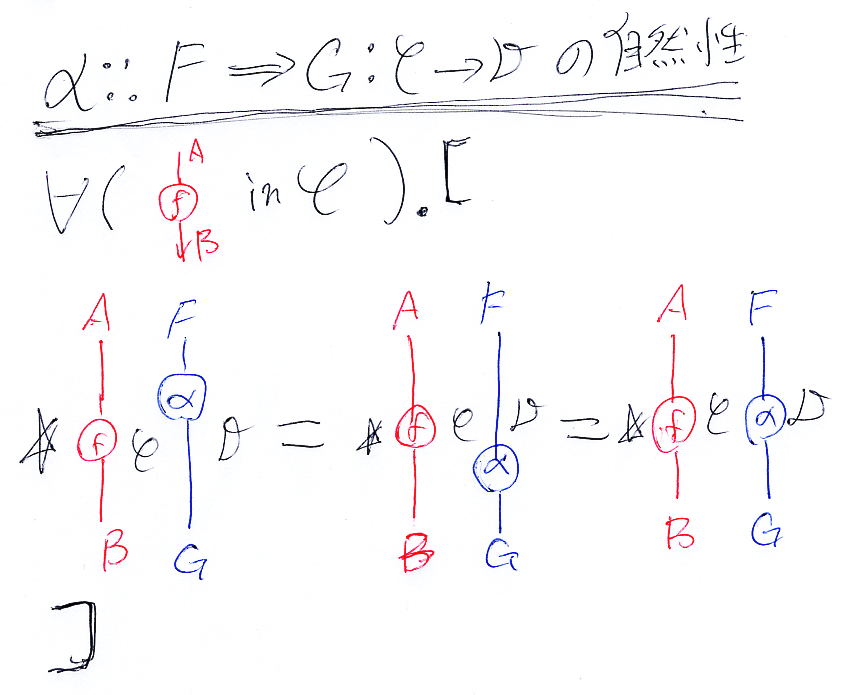
絵のレイアウトをある程度保存して写し取ると:
縦方向の結合を';'を使って1次元的に書けば:
反図式順では:
等式を可換図式で書けば:
自然変換の横結合
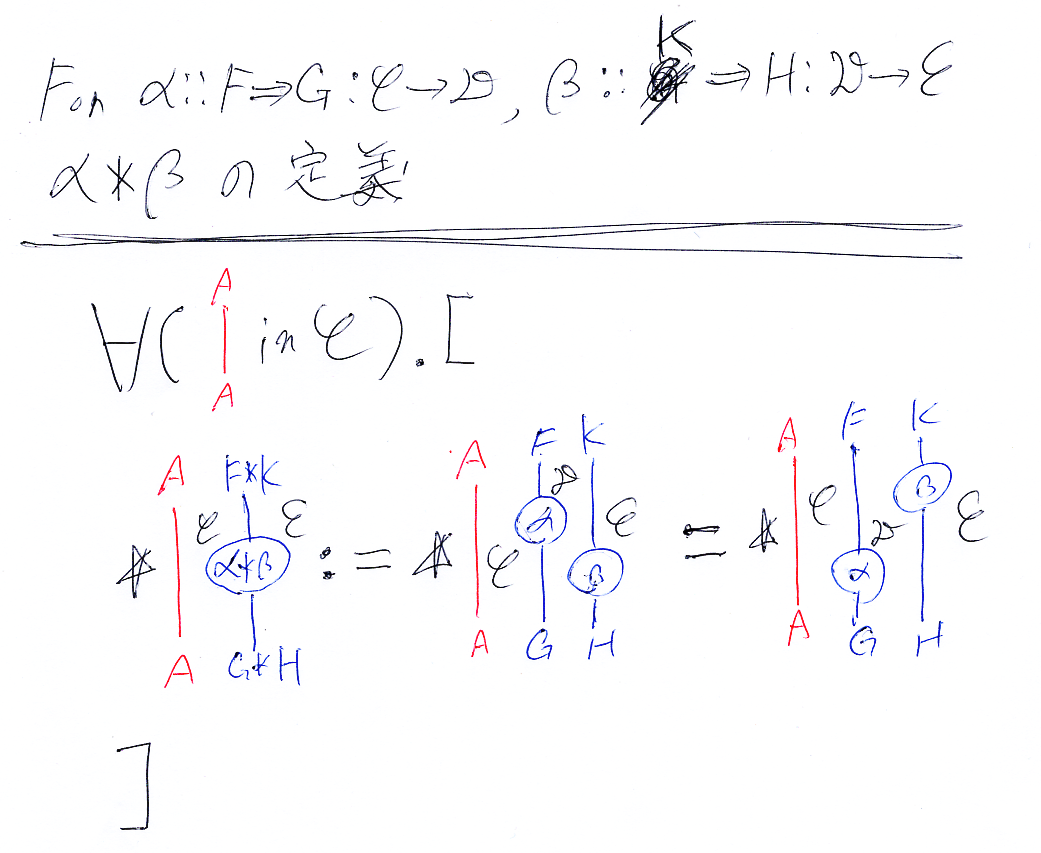
状況をペースティング図もどきで描くと:
定義の等式の第二項と第三項のあいだの等式を確認する。
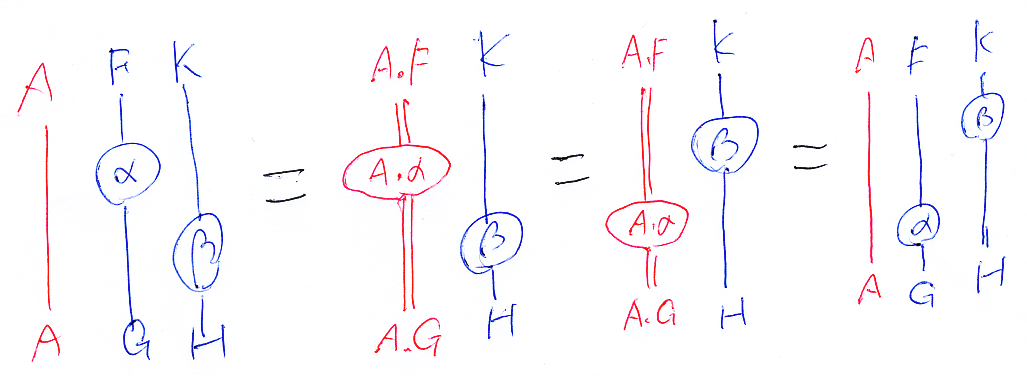
この等式の一部を可換図式(βの自然性)で書けば:
横結合の定義がwell-definedであることと、自然変換のエレベーター規則〈交替律〉が示せた。
記法とレイアウトは色々なので、上の可換図式(を含む命題)を、別な記法・レイアウトで描いてみる。
人によっては、Aを省略して次のような書き方を使う場合もある。もちろん、矢印方向や縦横の取り方はバラバラ。
ストライプ図ならば:
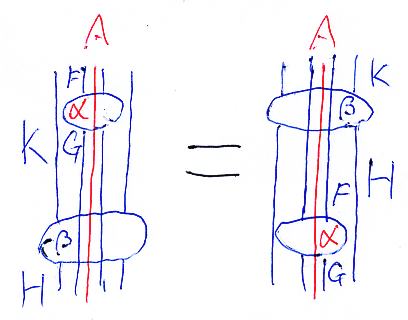
ストリング図とストライプ図の併用については:
圏の2-圏の構造(絵だけ)
圏の対象集合とホムセット(ホム集合)
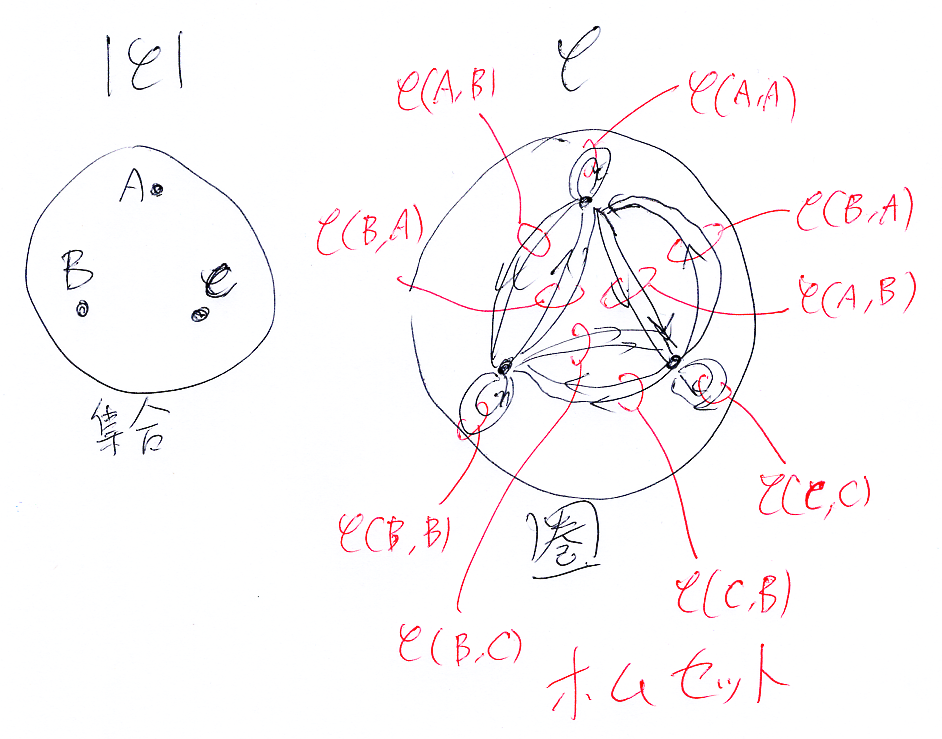
2-圏Catのホム圏である関手圏
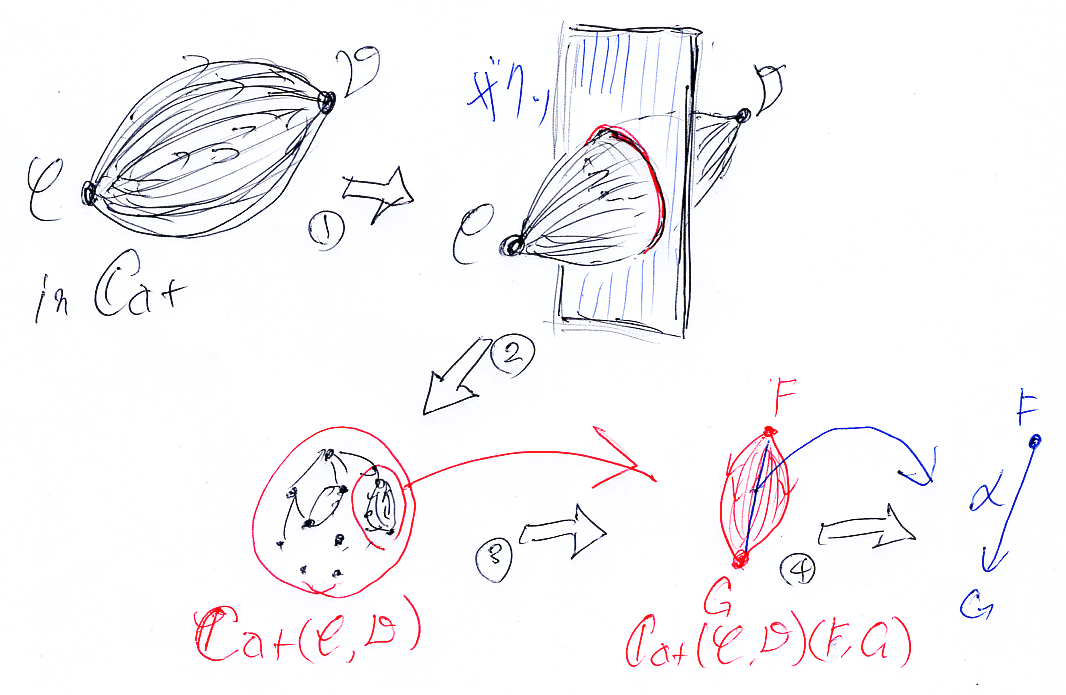
2-射の絵の描き方:
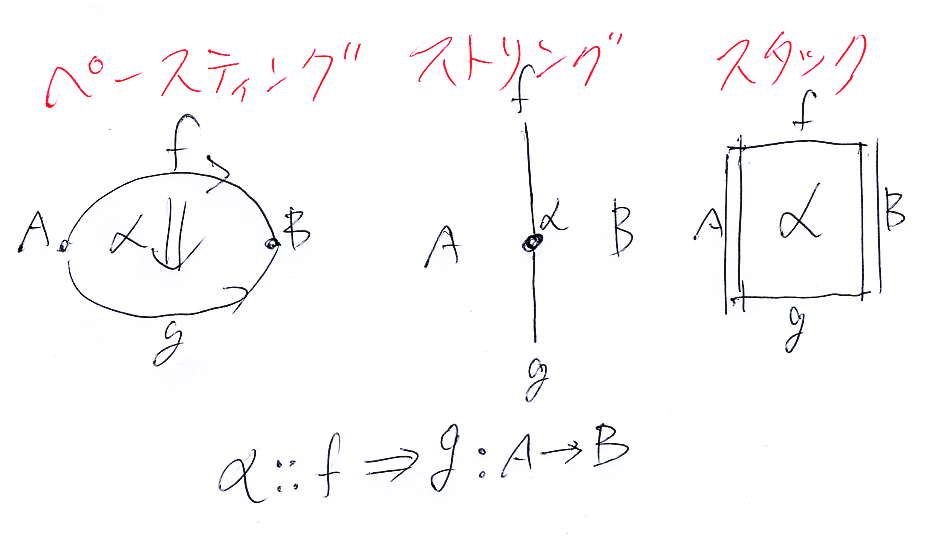
スタック図については:
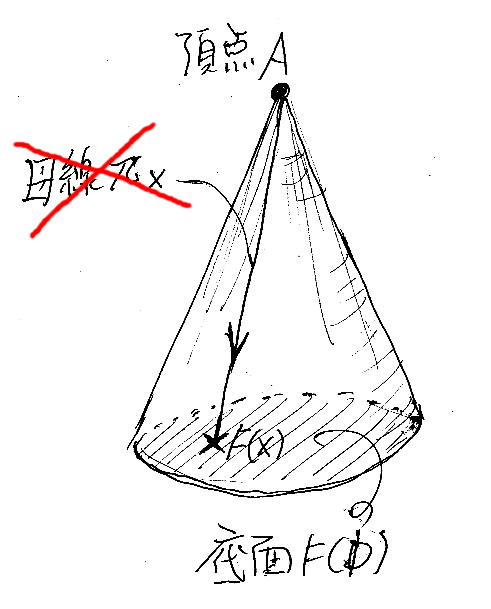
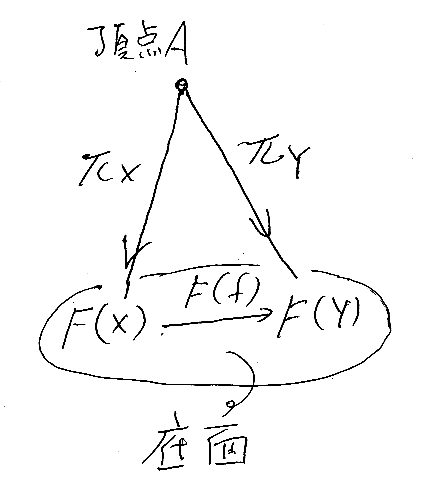
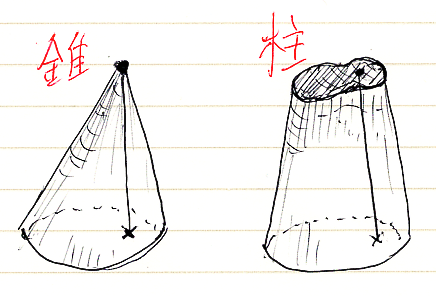
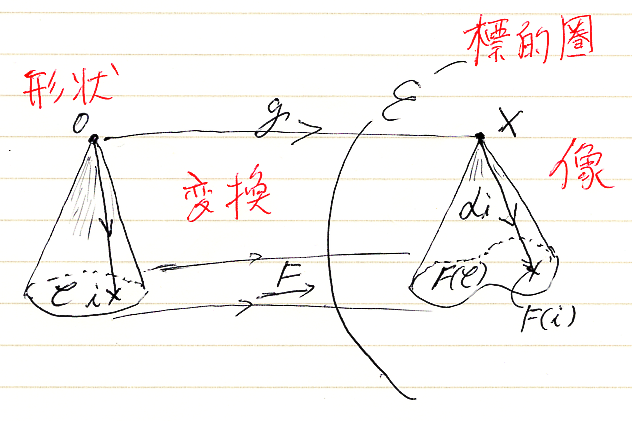
一時的に追加:錐